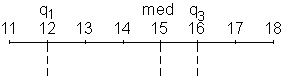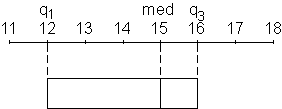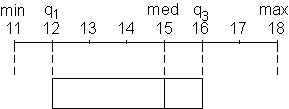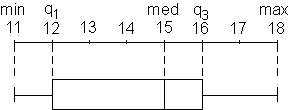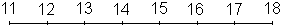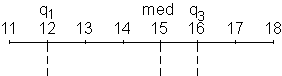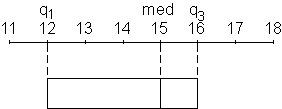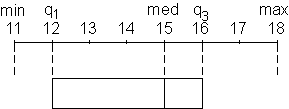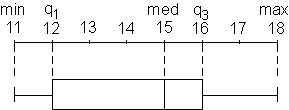|
In den vorigen Klassen hast du bereits gelernt, den "Mittelwert"
zu berechnen und du hast auch ganz bestimmt schon mehrere Male deinen
"Notendurchschnitt" berechnet.
- Beschreibe mit eigenen Worten, wie du deinen Notendurchschnitt berechnet
hast!
- Beschreibe mithilfe einer Formel, wie du deinen Notendurchschnitt
berechnet hast!
|
Der Mittelwert ist eine der wichtigsten Größen in der beschreibenden
Statistik. In den nachfolgenden Aufgaben lernst du, ihn zu berechnen und zu
interpretieren.
|
Rufe die Flash-Lernhilfe
 Was
ist der Mittelwert? Was
ist der Mittelwert?
auf und wähle die Einstellung "Mittelwert von 2 Zahlen"!
- Ermittle mithilfe dieses Tools den Mittelwert der Zahlen 0.2 und 1.6.
Überprüfe das Resultat durch eine Rechnung!
- Ermittle mithilfe dieses Tools den Mittelwert der Zahlen 0.5 und 0.6.
Überprüfe das Resultat durch eine Rechnung!
- Ermittle mithilfe dieses Tools den Mittelwert der Zahlen -0.5 und
0.5.
Überprüfe das Resultat durch eine Rechnung!
- Ermittle mithilfe dieses Tools den Mittelwert der Zahlen 0.5 und 2.
Wie groß ist der Abstand der beiden Zahlen vom Mittelwert?
- Wähle nun selbstständig drei beliebige Zahlpaare, ermittle
den Mittelwert dieser Paare mithilfe des Tools und überprüfe
das Resultat durch Rechnung!
Was kannst du nun über den Abstand der Paare vom Mittelwert sagen?
- Überzeuge dich nun durch weitere Beispiele davon, dass der Mittelwert
zweier Zahlen von jeder dieser beiden Zahlen den gleichen Abstand hat!
- Wie groß ist der Mittelwert zweier gleich großer Zahlen?
|
|
Rufe die Flash-Lernhilfe
 Was
ist der Mittelwert? Was
ist der Mittelwert?
auf und wähle die Einstellung "Mittelwert von 3 Zahlen"!
- Ermittle mithilfe dieses Tools den Mittelwert der Zahlen -0.8, 0.2
und 1.8.
Überprüfe das Resultat durch eine Rechnung!
- Wie musst du die mittlere der drei Zahlen wählen, damit sie mit
dem Mittelwert aller drei Zahlen übereinstimmt?
- Für die Arbeit in einer 3er-Gruppe: Messt eure Körpergrößen
(in Meter) und ermittelt mithilfe dieses Tools eure mittlere Körpergröße!
|
|
Rufe die Flash-Lernhilfe
 Was
ist der Mittelwert? Was
ist der Mittelwert?
auf und wähle die Einstellung "Mittelwert von 4 Zahlen"!
- Stelle mit drei der Zeiger die Zahlen 0.3, 0.4 und 0.5 ein und beobachte,
wie der Mittelwert von der vierten Zahl abhängt!
- Stelle drei der Zeiger auf die Zahl 0.4 ein (sie liegen dann übereinander)
und verändere die vierte Zahl beliebig.
Kannst du mit einfachen Worten beschreiben, wo der Mittelwert der vier
Zahlen liegt?
- Stelle die vier Zeiger so ein, dass sie den Mittelwert 0 haben! Kannst
du zwei verschiedene Einstellungen mit Mittelwert 0 angeben?
- Für die Arbeit in einer 4er-Gruppe: Messt eure Körpergrößen
(in Meter) und ermittelt mithilfe dieses Tools eure mittlere Körpergröße!
|
|
Rufe die Flash-Lernhilfe
 Was
ist der Mittelwert? Was
ist der Mittelwert?
auf und wähle die Einstellung "Mittelwert von 4 Zahlen"!
- Überzeuge dich durch einige Beispiele davon, dass der Mittelwert
nie kleiner als die kleinste und nie größer als die größte
der Zahlen ist, aus denen er gebildet wird!
- Stelle mit den fünf Zeigern die Zahlen 0, 0.5, 1, 1.5 und 2 ein!
Wie groß ist der Mittelwert? Verändere die Einstellung der
fünf Zeiger so, dass der Mittelwert erhalten bleibt. Wie viele
solcher Einstellungen findest du? Beschreibe deine Überlegungen
mit einfachen Worten!
- Wähle für vier Zeiger eine Einstellung zwischen 1 und 1.5
und verändere die fünfte Zahl beliebig! Beobachte die entsprechende
Veränderung des Mittelwertes und schreibe deine Beobachtung mit
einfachen Worten auf!
- Für die Arbeit in einer 5er-Gruppe: Messt eure Körpergrößen
(in Meter) und ermittelt mithilfe dieses Tools eure mittlere Körpergröße!
|
Die Berechnung des Mittelwerts lässt sich durch eine Formel ausdrücken.
Formel: Mittelwert (arithmetisches Mittel, Durchschnittswert)
In der ersten Aufgabe hast du die Formel für die Berechnung des
Mittelwertes (= arithmetisches Mittel) bereits verbal formuliert
und versucht, sie in mathematischer Schreibweise anzugeben. Hier wird
die Formel nochmals ausführlich entwickelt. Versuche, jeden Schritt
zu verstehen, und präge dir die Formel gut ein! Schreibe die Formeln
auf!
Der Mittelwert zweier Zahlen a
und b
ist definiert als
__
x |
|
|
|
|
| = |
a
+ b
2 |
= |
1. Wert + 2. Wert
Anzahl der Werte |
. |
Der Mittelwert dreier Zahlen a,
b und
c ist
definiert als
__
x |
|
|
|
|
| = |
a
+ b + c
3 |
= |
1. Wert + 2. Wert + 3. Wert
Anzahl der Werte |
. |
Formuliere eine analoge Formel für den Mittelwert von fünf
Zahlen!
Der Mittelwert von n
Zahlen x1,
x2,
x3,...
xn
ist definiert als
__
x |
|
|
|
|
|
| = |
x1
+ x2
+ x3
+ ... + xn
n |
= |
Summe
aller Werte
Anzahl der Werte |
. |
Beachte: Der Mittelwert wird auch manchmal mit anderen Buchstaben (wie
m oder m)
bezeichnet.
|
Nun ist es Zeit, die Berechnung und Interpretation des Mittelwerts ein bisschen
zu üben. Dabei kannst du dir einen Teil der Arbeit von einem elektronischen
Werkzeug abnehmen lassen.
- Die folgende Tabelle zeigt die Einnahmen eines Kinos während
einer bestimmten Woche:
| Mo |
Di |
Mi |
Do |
Fr |
Sa |
So |
| 290 € |
150 € |
135 € |
210 € |
280 € |
325 € |
300 € |
a.) Berechne die durchschnittlichen Einnahmen des Kinos während
dieser Woche!
b.) Du kennst bestimmt die Preise für Kinokarten. Kannst du abschätzen,
wie viele Kinokarten ungefähr in dieser Woche verkauft wurden?
- In einem Kaufhaus wurden aus den Kundendaten die Entfernungen der
Kunden zum Wohnort ermittelt.
a.) Was bedeutet das arithmetische Mittel der Entfernungen?
b.) Welcher Schluss kann gezogen werden, wenn der Mittelwert der Entfernungen
13,7 km beträgt?
- Ein neues Gesetz verschafft allen Betrieben ab einer Größe
von 25 Beschäftigten eine Prämie von 1000 €. Im Wahlkampf
frohlockt der Bürgermeister: "Wir werden viel Geld aufgrund
dieses Gesetzes bekommen, da der durchschnittliche Betrieb in unserer
Gemeinde 28,6 Beschäftigte hat!"
a.) Glaubst du ihm?
Ein kritische Bürgerin entgegnet: "Die Beschäftigungszahlen
in unseren 11 Betrieben betragen: 3, 4, 6, 6, 7, 11, 13, 20, 22, 23,
200. Ich kann Ihre Freude nicht teilen!"
b.) Warum ist sie anderer Meinung als der Bürgermeister?
- Die
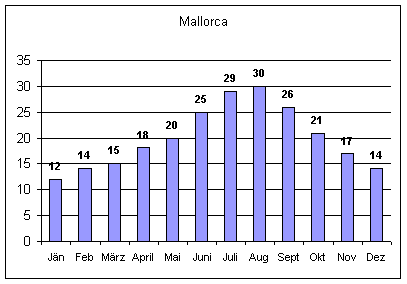 nebenstehende Graphik zeigt eine Monatsübersicht der Lufttemperatur
(in °C) in Mallorca. (Genau genommen handelt es sich für
jedes Monat um den Mittelwert der täglichen Tageshöchsttemperaturen.)
nebenstehende Graphik zeigt eine Monatsübersicht der Lufttemperatur
(in °C) in Mallorca. (Genau genommen handelt es sich für
jedes Monat um den Mittelwert der täglichen Tageshöchsttemperaturen.)
Wie hoch ist die Durchschnittstemperatur?
- Eine Datenliste bestehe aus drei Elementen.
a.) Gib eine mögliche Datenliste an, für die das arithmetische
Mittel 9 ist!
b.) Gib eine mögliche Datenliste an, für die das arithmetische
Mittel -3 ist!
- Die Elemente einer Datenliste heißen: u,
X,
p.
Drücke den Mittelwert durch u,
X
und p
aus!
- Schreibe den Mittelwert für die Datenliste a1,
a2,
a3,
a4,
a5...
ak
an!
Benutze dabei ein Werkzeug deiner Wahl:
|
Größere Datensätze lassen sich leichter mit elektronischen
Hilfsmitteln bearbeiten. Löse die folgende Aufgabe zum Beispiel mit dem
CAS-Rechner Voyage oder der Tabellenkalkulation Excel! Eigene Links zeigen dir,
wie du dabei vorgehst.
|
Mittelwertberechnung mit elektronischen Hilfsmitteln (z.B. Voyage, Excel)
In einem Jahr wurden in Venedig folgende Höchst- und Tiefstemperaturen
gemessen:
| Monat |
Höchsttemp. (°C) |
Tiefsttemp. (°C) |
| Jänner |
7 |
2 |
| Februar |
9 |
4 |
| März |
14 |
9 |
| April |
19 |
13 |
| Mai |
22 |
16 |
| Juni |
25 |
20 |
| Juli |
30 |
22 |
| August |
31 |
24 |
| September |
24 |
18 |
| Oktober |
18 |
13 |
| November |
12 |
10 |
| Dezember |
7 |
3 |
Ermittle
a.) den Mittelwert der Höchsttemperaturen
b.) den Mittelwert der Tiefsttemperaturen
Benutze dabei ein Werkzeug deiner Wahl! Hier ein paar Tipps:
|
Die folgende Aufgabe lässt sich nur mit elektronischen Hilfsmitteln sinnvoll
lösen, da es sich um sehr umfangreiches Datenmaterial handelt.
|
Mittelwertberechnung für sehr große Datenmengen
Rufe die
 Bevölkerungs-Daten Bevölkerungs-Daten 
in Excel auf und löse die in der Datei gestellten Aufgaben!
Benutze dabei ein Werkzeug deiner Wahl! Hier ein paar Tipps:
| |
 Excel
(Daten sortieren, Video) Excel
(Daten sortieren, Video) |
| |
 Excel
(Daten sortieren, Text/Grafik) Excel
(Daten sortieren, Text/Grafik) |
| |
 Excel
(Mittelwert berechnen, Video) Excel
(Mittelwert berechnen, Video) |
| |
 Excel
(Mittelwert berechnen, Text/Grafik) Excel
(Mittelwert berechnen, Text/Grafik) |
|
Median
|
Du kennst bereits eine statistische Kennzahl, das arithmetische Mittel.
Daneben gibt es noch andere Möglichkeiten, einen Mittelwert zu suchen:
In Turnen habt ihr sicher schon oft eine Stirnreihe gebildet und euch
dazu der Größe nach aufgestellt. Wie würdest du vorgehen,
wenn du ohne Maßband und möglichst rasch eine Person auswählen
sollst, die den durchschnittlichen Schüler bzw. die durchschnittliche
Schülerinnen in Hinblick auf die Körpergröße repräsentiert?
|
|
Nimm 7 Buntstifte und Bleistifte und lege sie vor dich hin. Sie sind
hoffentlich schon benutzt und haben unterschiedliche Länge! Sortiere
sie der Größe nach! Welcher Stift repräsentiert am besten
die durchschnittliche Länge der Stifte? Beantworte die Frage ohne
Messen und Rechnen!
Vergleiche deine Vorgangsweise mit folgender Festlegung:
Der Median (Zentralwert) ist jener Wert, der genau in
der Mitte aller Werte liegt, wenn man sie der Größe nach
ordnet.
Anders formuliert:
Höchstens die Hälfte der Werte ist kleiner als der Median
(Zentralwert).
Höchstens die Hälfte der Werte ist größer als der
Median (Zentralwert).
Bist du auch so vorgegangen?
Diese Zahl wird mit z (Zentralwert) oder mit der Abkürzung
med (Median) bezeichnet.
Miss nun die Längen der Stifte ab und schreibe die Werte vom kleinsten
zum größten Wert geordnet in deinem Heft auf:
| |
|
|
|
|
|
|
| kleinster Wert |
|
|
|
|
|
größter Wert |
Beschrifte den Median in der Tabelle!
Der kleinste Wert wird Minimum (min) genannt.
Der größte Wert wird Maximum (max) genannt.
Entferne nun einen beliebigen Stift, sodass nur noch 6 Stifte übrig
bleiben! Welchen Wert gibst du jetzt als Median an?
Vergleiche deine Überlegung mit folgender Festlegung:
Bei gerader Anzahl von Werten nimmt man des arithmetische Mittel
der Nachbarwerte in der Mitte der geordneten Liste.
Fülle die Tabelle aus:
| |
|
|
|
|
|
| kleinster Wert |
|

 |
|
größter Wert |
| |
|
|
|
|
| |
|
Median |
|
|
|
Lies die folgende Definition sorgfältig durch und notiere dir die wichtigsten
Informationen im Heft.
|
Der Median (Zentralwert) ist jener Wert, der genau in der
Mitte aller Werte liegt, wenn man sie der Größe nach ordnet.
Diese Zahl wird mit z (Zentralwert) oder mit der Abkürzung
med (Median) bezeichnet.
Bestimmen des Medians (Zentralwertes):
Bei ungerader Anzahl von Werten nimmt man genau jenen Wert,
der in der Mitte der geordneten Liste steht.
Bei gerader Anzahl von Werten nimmt man des arithmetische Mittel
der beiden Nachbarwerte in der Mitte der geordneten Liste.
Es gilt daher:
Höchstens die Hälfte der Werte ist kleiner als der Median (Zentralwert).
Höchstens die Hälfte der Werte ist größer als der
Median (Zentralwert).
Der kleinste Wert wird Minimum (min) genannt.
Der größte Wert wird Maximum (max) genannt.
|
|
Rufe die Flash-Lernhilfe
 Zentral-
und Streuungsmaße Zentral-
und Streuungsmaße
auf und wähle (durch Anklicken) die beiden Einstellungen "Median"
und "Mittelwert" aus! Die beiden Begriffe werden dann mit Pfeilen
markiert. Stelle außerdem das Beispiel 5 (Ausreißer) ein!
Die Zahl der Datenwerte sollte nun 10 betragen.
- Lies die eingestellten Datenwerte, den Median (Zentralwert, blauer
Strich) und den Mittelwert (roter Strich) ab!
- Welches der beiden Zentralmaße ist größer - der Median
oder der Mittelwert?
- Welcher Datenwert hebt sich von den anderen Werten ab?
Anmerkung: Einen solchen stark abweichenden Wert nennt man "Ausreißer".
Es kann sich dabei zum Beispiel um einen Messfehler handeln.
- Beobachte nun, wie sich statistische Ausreißer auf die beiden
Kenngrößen Median (Zentralwert) und Mittelwert auswirken!
Ziehe dazu den Datenpunkt ganz rechts (=Ausreißer) mit gedrückter
Maustaste quer über die anderen Datenpunkte ganz nach links! Beschreibe
in Worten, was du bei Median und Mittelwert beobachtest!
- Stelle den Ausreißer so ein, dass Median und Mittelwert gleich
groß sind! Notiere die entsprechenden Werte für den "Ausreißer",
den Median und den Mittelwert! Würdest du immer noch von einem
"Ausreißer" sprechen? Begründe deine Antwort!
- Welche Kennzahl, Median oder Mittelwert, reagiert stärker
auf Ausreißer? Welche Erklärung hast du dafür?
|
- a) Herr Marek notiert an verschiedenen Tagen die Zeiten (in Minuten),
die er für seinen Weg in die Arbeit benötigt:
55, 56, 51, 56, 49, 58, 55, 56, 56, 50.
Wie lange benötigt er durchschnittlich? Berechne dazu den Median
(Zentralwert) und den Mittelwert und vergleiche die beiden Werte.
b) Streiche nun den Wert 58 aus der Liste und ersetze ihn durch 70 (wegen
einer Baustelle musste Herr Marek einen Umweg in Kauf nehmen).
Wie lange benötigt er nun im Mittel? Berechne wieder den Median
und den Mittelwert. Vergleiche die beiden Werte mit jenen Werten aus
a). Was fällt dir auf? Verfasse eine Erklärung für deine
Beobachtung!
- Norbert und Sabine vergleichen ihre Schularbeitsnoten des 1.Semesters.
Sie wollen ermitteln, wer von ihnen bei den Schularbeiten besser abschnitt.
Norbert D: 3, 4, 3 M:
2, 2, 1 E: 2, 3, 2
Sabine D: 2, 3, 1 M:
1, 1, 2 E: 5, 5, 4
Ermittle für beide einzeln den Mittelwert und den Median. Wer war
deiner Meinung nach besser? Welchen Wert bzw. welche Werte ziehst du
für dein Urteil heran? Warum?
- Gegeben ist folgende Liste von 11 Datenwerten:
1,0 - 1,2 - 1,6 - 1,6 - 1,6 - 1,8 - 2,0 - 2,6 - 2,8 - 2,8 - 3,0.
Wie groß sind Median und Mittelwert?
Verändere genau einen Datenwert so, dass der Mittelwert kleiner
ist als der Median! Gib die geänderten Werte an!
Für Tüftler: Ändere genau einen Datenwert so, dass Median
und Mittelwert gleich groß sind!
Hier ein Werkzeug-Tipp:
|
Du wendest jetzt das neue Wissen auf einen sehr großen Datensatz an,
den du mit einem geeigneten Hilfsmittel bearbeitest.
|
Rufe die
 Bevölkerungs-Daten Bevölkerungs-Daten 
in Excel auf und löse die in der Datei gestellten Aufgaben!
Benutze dabei ein Werkzeug deiner Wahl! Hier ein paar Tipps:
| |
 Excel
(Daten sortieren, Video) Excel
(Daten sortieren, Video) |
| |
 Excel
(Daten sortieren, Text/Grafik) Excel
(Daten sortieren, Text/Grafik) |
| |
 Excel
(Median ermitteln, Video) Excel
(Median ermitteln, Video) |
| |
 Excel
(Median ermitteln, Text/Grafik) Excel
(Median ermitteln, Text/Grafik) |
|
Quartile
Um genauere Aussagen über die Verteilung von Daten treffen zu können,
sind neben den beiden Zentralmaßen Mittelwert und Median sowie den Streuungsmaßen
Minimum und Maximum weitere Kennzahlen notwendig. Lies den folgenden Text und
notiere dir zunächst die neuen Begriffe und ihre Bedeutung!
|
Was du schon weißt: Eine Liste von Datenwerten wird der Größe
nach geordnet. Der Median (Zentralwert) teilt diese geordnete Liste
der Datenwerte in eine untere und eine obere Teilliste.
(Bei einer ungeraden Zahl von Datenwerten entspricht der Median
dem mittleren Wert. Beim Teilen in untere und obere Teilliste wird dann
dieser Wert nicht berücksichtigt).
Nun werden die beiden Teillisten weiter unterteilt:
- Das untere Quartil (auch: 1.Quartil q1) ist der Median
der unteren Teilliste.
- Das obere Quartil (auch: 3.Quartil q3) ist der Median
der oberen Teilliste.
- Der Median (Zentralwert) entspricht dann dem mittleren
Quartil (auch: 2.Quartil q2).
Die Idee besteht also darin, die Datenwerte in vier Klassen aufzuteilen:
- Ein Viertel der Werte liegt unterhalb des unteren Quartils q1.
- Ein Viertel der Werte liegt zwischen dem unteren Quartil q1 und dem
Median.
- Ein Viertel der Werte liegt zwischen dem Medien und dem oberen Quartil
q3.
- Ein Viertel der Werte liegt oberhalb des oberen Quartils q3.
Im mittleren Bereich zwischen unterem und oberen Quartil liegen 50% der
Datenwerte, die sogenannten "mittleren 50% der Datenwerte".
|
In der folgenden Übung lernst du die Bedeutung des unteren und oberen
Quartils kennen.
|
Rufe die Flash-Lernhilfe
 Zentral-
und Streuungsmaße Zentral-
und Streuungsmaße
auf und wähle (durch Anklicken) die beiden Einstellungen "Median"
und "Quartile" aus! Die beiden Begriffe werden dann mit Pfeilen
markiert. Stelle außerdem das Beispiel 1 (Median und Quartile) ein!
Die Zahl der Datenwerte sollte nun 7 betragen.
- Lies den Median (Zentralwert) in der Anzeige ab! Schreibe die eingestellten
Datenwerte geordnet auf und markiere den Median!
- Welche Datenwerte gehören nun zur unteren Teilliste? (Beachte:
Der Median zählt nicht mit!) Bestimme nun in dieser Teilliste wieder
den Median! Dieser Wert ist das untere Quartil oder das 1.Quartil q1.
Der Wert sollte mit dem linken Wert in der Anzeige übereinstimmen.
Die Quartile sind durch senkrechte grüne Linien dargestellt.
- Welche Datenwerte gehören zur oberen Teilliste? Der Median zählt
wieder nicht mit. Bestimme abermals den Median dieser Teilliste! Du
erhältst so das obere Quartil oder 3.Quartil q3. Der Wert sollte
mit dem rechten Wert in der Anzeige übereinstimmen.
- Ziehe den größten Datenwert (3,3 ganz rechts) nach links
und beobachte, wann sich die Werte für oberes Quartil, Median und
unteres Quartil ändern! Notiere deine Antwort!
- Wähle nun Beispiel 2 (Median und Quartile) aus! Notiere die angezeigten
Datenwerte und ermittle händisch Median, unteres und oberes Quartil!
Vergleiche dein Ergebnis mit den Werten in der Anzeige!
|
In den Übungsaufgaben ermittelst du nun die Werte selbst. Tipps, wie du
unteres und oberes Quartil ermitteln kannst, findest du bei der Definition.
- Herr Marek notiert an verschiedenen Tagen die Zeiten (in Minuten),
die er für seinen Weg in die Arbeit benötigt:
55, 56, 51, 56, 25, 58, 55, 56, 56, 50, 52.
a) Berechne den Median (Zentralwert). Formuliere einen Satz, der ausdrückt,
was der Wert des Medians in diesem Beispiel bedeutet!
b) Ermittle das Minimum und das Maximum, das untere und obere Quartil!
c) Herr Marek vertraut dem kleinsten Wert nicht und streicht ihn aus
der Liste. Ermittle Median und Quartile der neuen Datenliste! Vergleiche
die neuen Werte mit den Werten der ersten Liste und beschreibe deine
Beobachtungen! Hast du eine Erklärung dafür?
d) Kannst du einen möglichen Grund nennen, warum Herr Marek den
kleinsten Wert aus der Liste für unwahrscheinlich hält? Worauf
könnte der Wert zurückzuführen sein?
- Gegeben ist folgende Liste von 12 Datenwerten:
1,0 - 1,2 - 1,6 - 1,6 - 1,6 - 1,8 - 2,0 -2,6 - 2,8 - 2,8 - 3,0 - 1,4.
Wie groß sind Median und Mittelwert?
Verändere genau einen Datenwert so, dass der Mittelwert kleiner
ist als der Median. Gib die geänderten Werte an!
Für Tüftler: Ändere genau einen Datenwert so, dass Median
und Mittelwert gleich groß sind!
- Die Auswertung der Körpermassen von 100 Katzen ergab folgende
Ergebnisse:
- Die leichteste Katze wog 1,2 kg, die schwerste Katze 4,2 kg.
- 50% der Katzen waren leichter als 3,1 kg und 50% waren schwerer
als 3,1 kg.
- Die mittlere Hälfte der Katzen wog zwischen 2,5 kg und 3,5
kg.
- Ein Viertel der Katzen wog mindestens 1,2 kg und höchstens
2,5 kg.
- 25 Katzen brachten mindestens 3,5 kg und höchstens 4,2 kg
auf die Waage.
Beantworte mithilfe dieser Aussagen folgende Fragen:
a) Welchen Wert hat der Median (Zentralwert)?
b) Wie groß sind Minimum und Maximum der erhobenen Werte?
c) Wie groß sind unteres und oberes Quartil?
d) Wie viele Katzen waren leichter als 3,1 kg?
e) Wie viele Katzen waren schwerer als 2,5 kg?
f) Es sind nicht alle der oben angeführten Sätze notwendig,
um Minimum, Maximum, Median und Quartile eindeutig bestimmen zu können.
Verringere die oben angeführten Sätze soweit wie möglich!
Hier ein Werkzeug-Tipp:
|
Das neue Wissen wendest du jetzt wieder auf den Datensatz zur österreichischen
Bevölkerung an.
|
Rufe die
 Bevölkerungs-Daten Bevölkerungs-Daten 
in Excel auf und löse die in der Datei gestellten Aufgaben!
Benutze dabei ein Werkzeug deiner Wahl! Hier ein paar Tipps:
| |
 Excel
(Daten sortieren, Video) Excel
(Daten sortieren, Video) |
| |
 Excel
(Daten sortieren, Text/Grafik) Excel
(Daten sortieren, Text/Grafik) |
| |
 Excel
(Quartile ermitteln, Video) Excel
(Quartile ermitteln, Video) |
| |
 Excel
(Quartile ermitteln, Text/Grafik) Excel
(Quartile ermitteln, Text/Grafik) |
|
BoxPlots
|
Ein BoxPlot (Kastenschaubild) ist ein Diagramm, das von
einer Datenliste lediglich das Minimum, das Maximum, den Median, das untere
und das obere Quartil zeigt.
Anhand eines Beispiels: Am 03.04.2000 wurden an verschiedenen Orten die
Tageshöchstwerte gemessen und ausgewertet.
- Die gemessenen Werte liegen zwischen min = 11° und max = 18°
C.
- In 50% der Orte liegt der Tageshöchstwert zwischen q1 = 12°
und q3 = 16° C.
- 25% der Werte liegen zwischen min = 11° und q1 = 12° C.
- In einem Viertel der Orte liegt der Tageshöchstwert zwischen
q1 = 12° und med = 15° C.
- 25% der erhobenen Daten liegen zwischen q3 = 16° und max = 18°
C.
Arbeitsschritte zum Erstellen des Boxplots:
|
Skala zeichnen |
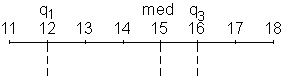 |
Werte für den Kasten in der Skala eintragen |
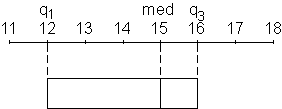 |
Kasten zeichnen |
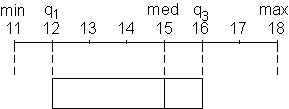 |
Begrenzungswerte in der Skala eintragen |
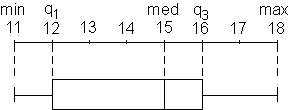 |
Schaubild fertig stellen |
Hier ein paar Werkzeug-Tipps:
|
|
Schülerinnen gaben bei einer Befragung an, wie viele Tage sie in
den Sommerferien auf Urlaub waren. Die Auswertung ergab folgende Werte:
min = 0 Tage
max = 60 Tage
med = 20 Tage
q1 = 10 Tage
q3 = 25 Tage
Zeichne zu diesem Beispiel einen Boxplot! Nimm auf der Skala 2 mm für
1 Tag!
|
Wenn du eine gerade Katalognummer hast, bearbeitest du Beispiel B. Wenn du
eine ungerade Katalognummer hast, bearbeitest du Beispiel C.
|
100 ausgewachsene Katzen wurden gewogen. Die Auswertung ergab folgenden
Boxplot:
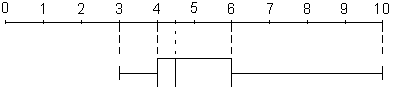
- Fülle (unten stehenden) den Lückentext aus!
- Tausche ihn mit jemandem aus, der das Beispiel C bearbeitet
hat!
- Zeichne zum erhaltenen Text den Boxplot!
- Tauscht die Texte mit dem gezeichneten Schaubild wieder aus!
- Vergleiche das erhaltene Schaubild mit dem eigenen!
- Falls es nicht übereinstimmt, versuche herauszufinden, wo der
Fehler liegt!
Lückentext:
100 ausgewachsene Katzen wurden gewogen. Die Auswertung ergab Folgendes:
Die Hälfte der leichtgewichtigen Katzen wiegt zwischen ...............
und ................. kg.
Die 25 schwersten Katzen wiegen von ............... bis ...............
kg.
25% der leichtesten Katzen wiegen unter ............... kg.
|
Wenn du eine gerade Katalognummer hast, bearbeitest du Beispiel B. Wenn du
eine ungerade Katalognummer hast, bearbeitest du Beispiel C.
|
100 Schüler einer Sportschule wurden nach ihrem Zeitaufwand (in
Minuten) für ihre sportliche Betätigung pro Woche befragt.
Die Auswertung ergab folgenden Boxplot:

- Fülle den (unten stehenden) Lückentext aus!
- Tausche ihn mit jemandem aus, der das Beispiel B bearbeitet
hat!
- Zeichne zum erhaltenen Text den Boxplot!
- Tauscht die Texte mit dem gezeichneten Schaubild wieder aus!
- Vergleiche das erhaltene Schaubild mit dem eigenen!
- Falls es nicht übereinstimmt, versuche herauszufinden, wo der
Fehler liegt!
Lückentext:
100 Schüler einer Sportschule wurden nach ihrem Zeitaufwand (in
Minuten) für ihre sportliche Betätigung pro Woche befragt.
Die Auswertung ergab Folgendes:
Die 25% der eifrigsten Sportler trainieren mehr als ................
Minuten.
Die Hälfte der Sportler mit hoher Trainingszeit wendet zwischen
................ und ................ Minuten für die Sportausübung
auf.
Die 25 Sportler mit der geringsten Trainingszeit trainieren von ...............
bis ................ Minuten.
|
Arbeitet zu zweit! Wer jünger ist, erklärt die Vorgangsweise, wie
dieser Boxplot gezeichnet wird. Wer älter ist, erklärt, was aus einem
Boxplot abgelesen werden kann.
|
Erkläre anhand der folgenden Zeichnungen, wie ein Boxplot gezeichnet
wird! Beschreibe in eigenen Worten, was aus dem fertigen Boxplot abgelesen
werden kann!
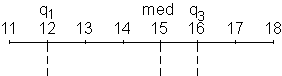
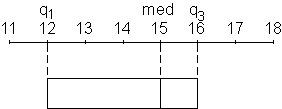
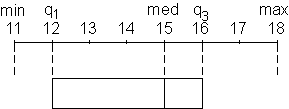
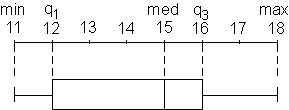
|
|
Bearbeite mindestens eines der folgenden Beispiele am Papier! Verwende
für mindestens eines der Beispiel Excel oder einen CAS-Rechner!
- Herr Marek notiert an verschiedenen Tagen die Zeiten (in Minuten),
die er für seinen Weg in die Arbeit benötigt:
55, 56, 51, 56, 49, 58, 55, 56, 56, 50.
Zeichne einen Boxplot!
- Hans Heißhunger erkundigt sich in verschiedenen Lokalen, wie
viel die angebotenen Mittagsmenüs kosten, und erhält folgende
Daten (Preise in Euro):
5,00 - 4,50 - 5,00 - 5,20 - 6,00 - 4,90 - 4,50 - 5,20 - 8,00 - 4,80
- 4,60 - 5,10 - 5,50 - 5,90.
Ermittle Minimalwert, Maximalwert, Zentralwert, 1.Quartil und 3.Quartil!
Zeichne einen Boxplot!
In welchem Preisintervall liegen 50% aller Menüpreise der mittleren
Preiskategorie?
- Gegeben ist folgende Liste von 12 Datenwerten:
1,0 - 1,2 - 1,6 - 1,6 - 1,6 - 1,8 - 2,0 -2,6 - 2,8 - 2,8 - 3,0 - 1,4.
Erstelle einen Boxplot und gib die Kenngrößen Minimum, Maximum,
Median, unteres Quartil und oberes Quartil an!
|
|
Rufe die Flash-Lernhilfe
 Box-Plots Box-Plots
auf! Gib in das linke Textfeld oberhalb der Skala als untere Grenze für
die Datenwerte 0 ein und in das rechte Textfeld den Wert 50. Wenn du die
Daten in den drei Datenfeldern händisch eingibst, trenne die Zahlenwerte
durch Leerzeichen! Verwende keine Beistriche! Mit dem Plot-Schalter werden
die Boxplots gezeichnet.
3 SchülerInnen führen eine Befragung zur Höhe des Taschengeldes
in drei verschiedenen Orten durch. Sie geben ihre Datenwerte an:
Ort A (Datensatz 1): 5 10 15 20 35 20 45 30 25 20 10 10 20 10 5 15 20
10
Ort B (Datensatz 2): 15 0 10 5 5 25 30 40 30 15 25 50
Ort C (Datensatz 3): 5 10 20 25 20 10 25 20 25 30 20 25
Beantworte folgende Fragen mithilfe der grafischen Darstellung im obigen
Tool (du kannst die Daten durch Kopieren und Einfügen übertragen)
und drücke deine Überlegungen schriftlich aus! Vielleicht sind
auch verschiedene Antworten möglich.
- Lies für jeden Ort die Kenngrößen Minimum, Maximum,
Median, unteres und oberes Quartil ab!
- In welchem Ort sind die Unterschiede beim Taschengeld am geringsten?
In welchem Ort sind sie am größten?
- In welchem Ort bekommen die Kinder am wenigsten Taschengeld?In welchem
Ort wird am meisten Taschengeld bezahlt?
- In welchem Ort ist der Unterschied bei den mittleren 50% am größten?
- In welchem Ort gibt es im dritten Viertel die geringsten Unterschiede?
|
Standardabweichung
Lies die folgende Information Schritt für Schritt durch und wende die
Anleitung auf die 4 Datenwerte 1, 3, 5 und 7 an!
|
Neben der Spannweite und dem Quartilsabstand zwischen unterem und oberem
Quartil stellt die Standardabweichung ein weiteres Maß für
die Streuung dar. Sie gibt an, wie stark die Datenwerte im Durchschnitt
vom Mittelwert abweichen.
- Um sie zu ermitteln, berechnest du zunächst für jeden Datenwert
den Unterschied zum Mittelwert.
- Die Unterschiede werden einzeln quadriert.
- Anschließend wird aus den quadrierten Unterschieden die Summe
berechnet.
- Die Summe wird durch die Anzahl n der Datenwerte dividiert.
- Aus dem Ergebnis wird abschließend die Wurzel gezogen.
Vorgangsweise für vier Datenwerte a, b, c und d mit Mittelwert m:
- Unterschiede berechnen: (a - m), (b - m), (c - m ), (d - m)
- Quadrieren: (a - m)², (b - m)², (c - m)², (d - m)²
- Summe bilden: (a - m)² + (b - m)² + (c - m)² + (d -
m)²
- Division durch 4:
(a - m)² + (b - m)² + (c - m)² + (d - m)²
4
- Durch Ziehen der Quadratwurzel erhältst du die Standardabweichung
s:
| |
|
_______________________________ |
|
| s =
|
Ö |
(a - m)²
+ (b - m)² + (c - m)² + (d - m)²
4 |
|
Die Standardabweichung wird als Abweichung links und rechts vom Mittelwert
eingezeichnet:
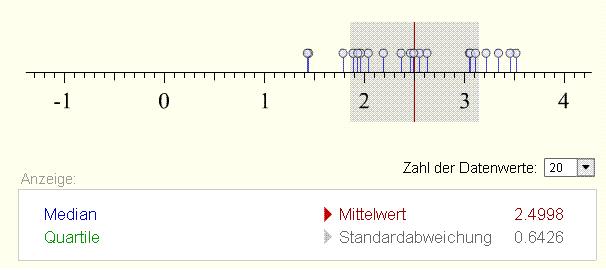
Im Bereich der Standardabweichung liegen in der Regel ungefähr 2/3
der Datenwerte.
Für n Datenwerte x1,
x2, … xn
mit Mittelwert m lautet die Formel:
|
|
_______________________________ |
|
| s =
|
Ö |
(x1
- m)2 + (x2 - m)2 + ... + (xn
- m)2
n |
|
Beachte: Die Standardabweichung wird auch manchmal mit dem Buchstaben
s bezeichnet.
|
In der folgenden Übung untersuchst du, wie sich Daten auf die Standardabweichung
und auf unteres und oberes Quartil auswirken.
|
Rufe die Flash-Lernhilfe
 Zentral-
und Streuungsmaße Zentral-
und Streuungsmaße
auf und wähle durch Anklicken "Mittelwert" und "Standardabweichung"
aus. Die beiden Begriffe werden mit Pfeilen markiert! Stelle außerdem
das Beispiel 4 (Zufallsgenerator) ein! Die Zahl der Datenwerte sollte
nun 20 betragen.
- Ein Zufallsgenerator würfelt Datenwerte, wie sie auch in der
Realität häufig vorkommen. Zähle ab, wie viel Prozent
der Daten vom Mittelwert nicht weiter entfernt sind als eine Standardabweichung!
Wenn du noch einmal "Beispiel 4 (Zufallsgenerator)" wählst,
wird erneut gewürfelt. Wiederhole diese Übung mehrere Male,
indem du das Beispiel 4 immer wieder neu auswählst! Fällt
dir eine (ungefähre) Gesetzmäßigkeit auf?
- Wähle nun im unteren Drop-Down-Menü "Beispiel 4 (Zufallsgenerator)"
und als Ansichten "Quartile" und "Standardabweichung"!
Vergleiche den Bereich der Standardabweichung (grau) mit dem Quartilsabstand
zwischen unterem und oberen Quartil (grün)!
Ist der (grüne) Bereich zwischen den Quartilen oder der durch die
Standardabweichung definierte (graue) Bereich größer? Wiederhole
diese Übung mehrere Male! Warum ist meistens der graue Bereich
größer?
- Wähle im unteren Drop-Down-Menü "Beispiel 5 (Ausreißer)"
und studiere, wie sich "Ausreißer" (d.h. stark abweichende
Datenwerte, die möglicherweise auf Messfehler zurückgehen)
auf die Standardabweichung auswirken! Ziehe dazu den Ausreißer
(ganz rechts bei 3.8) mit der Maus quer über die Daten bis ganz
nach links! Beobachte und erkläre, wie sich die Standardabweichung
dabei ändert. Wie empfindlich ist sie gegenüber Ausreißern?
Benutze ein Werkzeug deiner Wahl! Hier ein paar Tipps:
|
Als abschließende Übung berechnest du für zwei Datensätze
Mittelwert und Standardabweichung, um dadurch die vorhandenen Daten zu beurteilen
und Schlussfolgerungen zu ziehen.
|
Herr Strasser fährt täglich mit seinem Auto von seiner Wohnung
zu seinem Arbeitsplatz. Seine Fahrzeiten an verschiedenen Tagen findest
du in den folgenden Tabellen. Berechne die mittlere Fahrzeit und die Standardabweichung!
Route A:
| tägliche Fahrzeit (in min) |
| 58 |
| 43 |
| 44 |
| 49 |
| 40 |
| 60 |
| 42 |
| mittlere Fahrzeit m (in min): |
| Standardabweichung s (in min): |
Route B:
| tägliche Fahrzeit (in min) |
| 51 |
| 57 |
| 55 |
| 53 |
| 54 |
| 49 |
| 52 |
| mittlere Fahrzeit m (in min): |
| Standardabweichung s (in min): |
Vergleiche die beiden Ergebnisse! Welche Route würdest du Herrn
Strasser empfehlen? Schreibe einen kurzen Brief mit deinen Argumenten
an Herrn Strasser!
|
 nebenstehende Graphik zeigt eine Monatsübersicht der Lufttemperatur
(in °C) in Mallorca. (Genau genommen handelt es sich für
jedes Monat um den Mittelwert der täglichen Tageshöchsttemperaturen.)
nebenstehende Graphik zeigt eine Monatsübersicht der Lufttemperatur
(in °C) in Mallorca. (Genau genommen handelt es sich für
jedes Monat um den Mittelwert der täglichen Tageshöchsttemperaturen.)