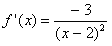Übungen zur Ableitung
Bei diesen Übungen bestimmst du die Steigung der Tangente an eine Funktion f(x) an einer allgemeinen Stelle x. Dazu berechnest du die Ableitung f'(x) mit Hilfe des Differentialquotienten.Übung 1)
|
a) Bestimme die
Ableitung der Funktion f(x)
= x2 - 2 händisch mit Hilfe des
Differentialquotienten in
deinem Heft (Tipp: siehe Übung 1c zum Differentialquotienten). Vergleiche dein Ergebnis mit der Funktion f'(x) im rechten
Fenster. b) Du siehst rechts die Funktion f(x) = x2 - 2 und ihre Ableitung f'(x). Außerdem ist f'(x0) an der Stelle x0 eingezeichnet, die du verändern kannst.
|
©
M.
Hohenwarter, 2005, erstellt
mit GeoGebra
|
Übung 2a)
Hier wird die Steigung der Tangente an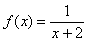 allgemein an
der Stelle x berechnet, also die Ableitung f'(x)
bestimmt. Vollziehe alle Schritte dieses Beispiels nach, indem du auf
den rechten Pfeil klickst.
allgemein an
der Stelle x berechnet, also die Ableitung f'(x)
bestimmt. Vollziehe alle Schritte dieses Beispiels nach, indem du auf
den rechten Pfeil klickst.| Definition der Ableitung: | 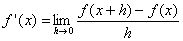 |
▼ |
| in f einsetzen: | 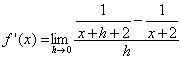 |
▼ |
| gemeinsamer Nenner: | 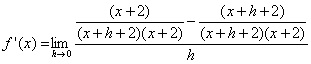 |
▼ |
| Zähler zusammenfassen: | 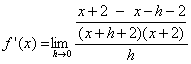 |
▼ |
| Zähler vereinfachen: | 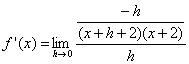 |
▼ |
| Doppelbruch auflösen: | 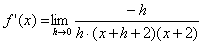 |
▼ |
| durch h kürzen: | 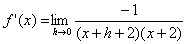 |
▼ |
| Grenzwertberechnung: | 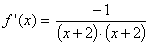 |
▼ |
| Nenner vereinfachen: | 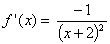 |
▼ |
Lösung: Die Steigung der Tangente an 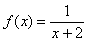 an
der Stelle x
ist
an
der Stelle x
ist
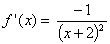 .
.
Oder anders gesagt: Die Ableitung von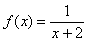 ist
ist
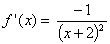 .
.
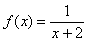 an
der Stelle x
ist
an
der Stelle x
ist
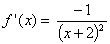 .
.Oder anders gesagt: Die Ableitung von
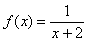 ist
ist
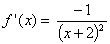 .
.Übung 2b)
Du siehst rechts
die Funktion f(x) und
ihre Ableitung f'(x).
Außerdem ist f'(x0)
an der Stelle x0
eingezeichnet, die
du verändern
kannst.
|
©
M.
Hohenwarter, 2005, erstellt
mit GeoGebra
|
Übung 3)
Bestimme die Ableitung der Funktion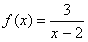 in deinem Heft.
Für welche Stellen ist die Steigung der Tangente an f(x) nicht
definiert?
in deinem Heft.
Für welche Stellen ist die Steigung der Tangente an f(x) nicht
definiert?Lösung: