Integration mit unbekannten Grenzen

Teil a)  Wie muss die obere Integrationsgrenze c gewählt werden, damit der Flächeninhalt unter dem Graph von
f: von x = 1 bis x = c genau dem halben Flächeninhalt von x = 1 bis x = 16 entspricht?

Please install Java 1.4 (or later) to use this page.

Aufgaben 

• Verschiebe die Gerade g so, dass der Flächeninhalt A₁ den Flächeninhalt A₂ halbiert!
  Lösung: c = 6,25 

• Berechne in deinem Heft die gesuchte obere Grenze c!
  

Lösung

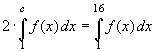
Teil b) Wie muss die obere Integrationsgrenze d gewählt werden, damit der Flächeninhalt A₂ unter dem Graph von
f: von x = 1 bis x = d genau dem doppelten Flächeninhalt A₁ von x = 1 bis x = 9 entspricht?

Please install Java 1.4 (or later) to use this page.

Aufgaben:  

• Verschiebe die Gerade g so, dass der Flächeninhalt A₁ gerade die Hälfte des Flächeninhalts A₂ ist!
  Lösung: d = 25 

• Löse dieses Beispiel analog zum Teil a) mit Papier und Bleistift!
  Die richtige Lösung ist aus der linken Konstruktion ersichtlich.