Hauptsatz: Beweis Teil (b)
|
Sei
die Funktion f im Intervall [a, b] stetig, dann gilt: |
||
| Beweis b): Anschauliche Begründung
Wie wir in Teil a gesehen haben, ist die Integralfunktion (Flächeninhaltsfunktion) A(x) eine Stammfunktion von f. Alle anderen Stammfunktion F(x) können sich deshalb nur um eine additive Konstante c von A(x) unterscheiden. F(x) = A(x) + c ( |
||
|
Aufgabe
|
||
| Formaler Beweis | ||
| Sei F(x) = A(x) + c | ||
|
Für x = a folgt: F(a) =
A(a) + c = |
=> F(a) = c ; | |
|
für x = b folgt:
F(b) = A(b) + c = |
=> 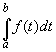 = F(b) - c = F(b) - F(a)
= F(b) - c = F(b) - F(a) |
|
|
q.e.d. |
||
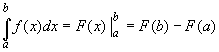
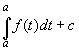 = 0 +
c
= 0 +
c