Erweiterter euklidischer Algorithmus

Der euklidische Algorithmus ist ein Verfahren, um den größten gemeinsamen Teiler zweier positiver ganzer Zahlen zu berechnen. Sind a und m zwei teilerfremde positive ganze Zahlen, so kann eine erweiterte Version dieses Algorithmus verwendet werden, um die "modulare Inverse von a mod m", d.h. jene (eindeutig bestimmte) positive Zahl b < m, die die Gleichung

a^.b mod m = 1

erfüllt, zu berechnen.

Die Basis für diese Aussage ist folgender Satz:

Satz: Sei d der größte gemeinsame Teiler der Zahlen a und b. Dann gibt es ganze Zahlen x und y mit der Eigenschaft, dass

d = xa + yb

Eine solche Darstellung wird Vielfachsummendarstellung des größten gemeinsamen Teilers d (von a und b) genannt.

Beispiel:
a = 16, b = 13, wir suchen jene Zahl c, sodass 13^.c mod 16 = 1
(wir gehen zunächst noch mit der "normalen" modularen Division vor).

  13*2 mod 16 = 10
  13*3 mod 16 =  7
  13*4 mod 16 =  4
  13*5 mod 16 =  1

Antwort: c = 5

Für höhere Zahlen wird die Variante "Durchprobieren" etwas mühsam - wir verwenden daher den Algorithmus:

Beispiel:
a = 160, b = 13 wir suchen die modulare Inverse zu 13 mod 160 (Probieren dauert hier schon etwas länger!). Laut dem Satz zur Vielfachsummendarstellung ist dies gleichbedeutend mit d = x*160 + y*13, das y wäre dabei unsere gesuchte Inverse.

Verfahren:

Wir suchen jene Zahl c, sodass 13^.c mod 160 = 1
Ablauf:

ggT
Umkehrung
Substitution

ggT: Zunächst wird mittels euklidischem Algorithmus der größte gemeinsame Teiler (hier bekannterweise 1) berechnet!

ggt(13,160)
160 = 12 * 13 +     4
           13 = 3 * 4 +     1
                    4 = 4 * 1 + 0
ggt(13,160) = 1

Umkehrung: Anschließend zäumen wir das Pferde von hinten auf - wir betrachten den Algorithmus von unten nach oben:
(dabei wird die letzte Zeile - die ja nur mehr eine Überprüfung darstellt, außer Acht gelassen)

1 = 13 - 3 * 4
             4 = 160 - 12 * 13

Substitution: Anschließend substituieren wir

1 = 13 - 3 * (160 - 12 * 13)
1 = 13 - 3 * 160 + 36 * 13
1 = 37 * 13 - 3 * 160

Die gesuchte modulare Inverse zu 13 mod 160 lautet 37 (13^.37 mod 160 = 1).

Kontrolle mit DERIVE: 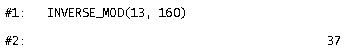Euklid1

Leichter geht die Berechnung (sowohl von Hand als auch in Hinblick auf Programmierung), wenn man folgende Variante des Algorithmus verwendet:

Alternatives Verfahren:

Wir suchen wieder jene Zahl c, sodass 13^.c mod 160 = 1
Ablauf:

  I:  160   1    0
 II:   13   0    1      III = I - 12* II (wie oft geht II in I)
III:    4   1  -12       IV =II -  3*III
 IV:    1  -3   37       inverse Modulare gefunden! 
                        
       1 =  -3*160 + 37*13
      13^.37 mod 160 = 1

Übung:
Finde mit Hilfe des erweiterten euklidischen Algorithmus

die modulare Inverse von 15 mod 26
die modulare Inverse von 5 mod 48

Alternative:
Finde mit Hilfe des erweiterten euklidischen Algorithmus (verwende die verbesserte automatisierte Variante)

die modulare Inverse von 15 mod 26
die modulare Inverse von 5 mod 48