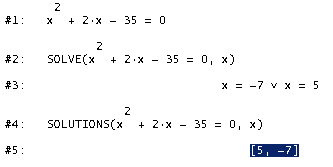DERIVE 6
Gleichungen in 1 Variablen
Inhalt
- Lösen einer linearen Gleichung
- SOLVE- und SOLUTIONS-Befehl
- Einschränkung der Lösungsmenge
- Numerisches Lösen von Gleichungen
Lösen einer linearen GleichungAufgabenstellung: Die lineare Gleichung a*x + b = c soll nach x aufgelöst werden.
DERIVE lässt uns dafür ad 1) Äquivalenzumformungen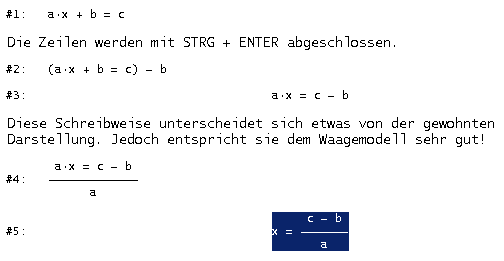
ad 2) SOLVE-BefehlDer SOLVE-Befehl verlangt nach der zu lösenden Gleichung und der Variablen (den Variablen), nach denen die Gleichung aufgelöst werden soll! 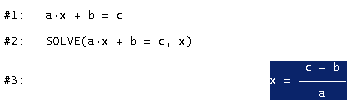
|
|||
SOLVE und SOLUTIONSDas erste Argument von SOLVE und SOLUTIONS ist die zu lösenden Gleichung (oder Ungleichung). Falls das Argument weder eine Gleichung noch Ungleichung ist, wird das Argument zu einer Gleichung gemacht, indem es gleich Null gesetzt wird. Das zweite Argument besteht aus der/den Lösungs-Variablen.
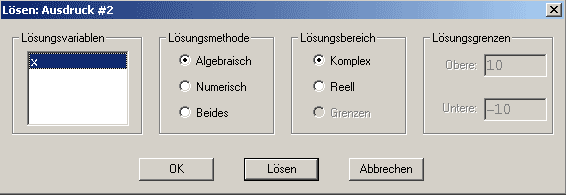
Hinweis - den Befehl "Lösen" (SOLVE) erhält man auch über das Menü (LÖSEN - AUSDRUCK) und mit Hilfe der Symbolleiste über das Symbol Bei Aufruf über das Menü öffnet sich folgender Dialog:
|
|||
Einschränkung der LösungsmengeWie man im Menü erkennen kann, unterscheidet DERIVE zwischen reellen und komplexen Lösungen. Der Variablenbereich lässt sich im Allgemeinen zwar weit genauer einschränken, jedoch lässt der SOLVE-Befehl keine weitere Feinjustierung zu. Tip: Wenn ein Variablenbereich festgelegt ist, kann dieser zur Anwendung gebracht werden, indem man die Lösung nochmals vereinfacht! Beispiel:Löse folgende Gleichung zuerst in der Grundmenge R, anschließend nur für positive reelle Zahlen: x2 + 2·x - 3 = 0 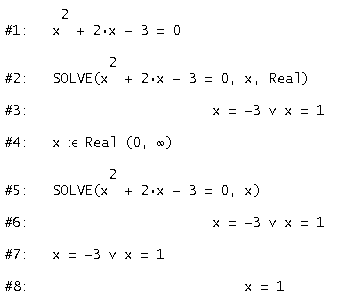
|
|||
Numerisches Lösen von GleichungenNicht alle Gleichungen lassen sich exakt lösen. Bereits Polynomgleichungen höherer Ordnung, aber auch div. trigonometrische Gleichungen, Exponentialgleichungen etc. lassen sich nur numerisch lösen. DERIVE bietet hierfür die Möglichkeit, entweder im Menü numerische auszuwählen, oder den Befehl NSOLVE zu verwenden. Bei einer Polynomgleichung mit numerischen Koeffizienten liefern NSOLVE und NSOLUTIONS alle reellen und komplexen Lösungen für die Gleichung. Für jeden anderen Gleichungstyp jedoch liefern NSOLVE und NSOLUTIONS jeweils nur eine Lösung. Die Suche kann durch händische Einschränkung des Lösungsbereichs noch weiter beschleunigt werden. Dazu werden nach der Variablen, nach der gelöst werden soll, noch die untere und oberer Schranke des Lösungsbereichs angegeben. 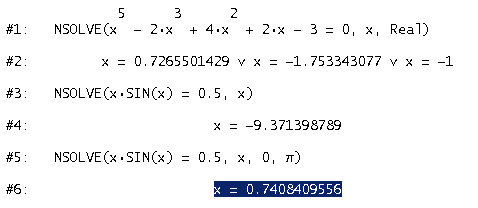
|
|||