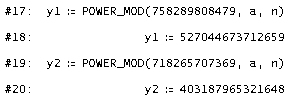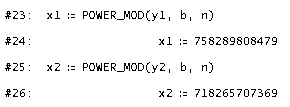Lösung - Numerikbeispiel 04

Der RSA-Algorithmus (der Name RSA kommt von Ronald Rivest, Adi Shamir und Leonard Adelman, den Entwicklern) basiert auf der Idee der Einwegfunktionen - wo eine Richtung leicht, die andere aber sehr schwierig (= langwierig) zu berechnen ist. Für eine einfache Entschlüsselung erfüllt der RSA zusätzlich auch die Bedingung einer Falltürfunktion - mit einer Zusatzinformation wird auch die Rückberechnung einfach!

Die dafür verwendete Funktion ist die Primfaktorenzerlegung einer langen Zahl. Wir erzeugen aus 2 Primzahlen ein Produkt, aus dem ohne Zusatzkenntnis diese beiden Primfaktoren nur sehr schwer = langwierig! - wieder herauszufiltern sind.

Grundvoraussetzung für die RSA-Verschlüsselung ist die Rechnung mit Restklassen (MODULO-Rechnung). Diese bildet mit einigen Sätzen der Zahlentheorie (Inverse von a modulo m - Lösung über den erweiterten euklidischen Algorithmus, Satz von Fermat-Euler) die Basis für den Algorithmus.

Verschlüsselung:

Wir wählen zwei Primzahlen p und q - das CAS unterstützt uns dabei mit dem Befehlen PRIME?(z) und NEXT_PRIME(z) bzw. PREVIOUS_PRIME(z) - der Überprüfung, ob eine Zahl z eine Primzahl ist bzw. der Berechnung der zur eingegebenen natürlichen Zahl z nächstgelegenen Primzahl größer z (NEXT) oder kleiner z (PREVIOUS).

Anschließend erzeugen wird die Produkte n = p . q und m = (p - 1) (q - 1)
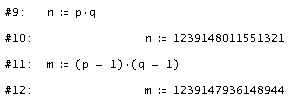p und q erzeugen n und m erzeugen

Wir brauchen neben n noch den zweiten Teil des öffentlichen Schlüssels, eine Zahl a, die teilerfremd zu m is. Die Überprüfung geht über die Frage: ist der größte gemeinsame Teiler gleich 1 --> GGT(m,a) = 1, DERIVE-Funktion GCD(a,b).
Wir wählen eine beliebige Zahl, erzeugen die nächstgelegene Primzahl und überprüfen den GGT.
a erzeugen

Damit ist mit den beiden Zahlen n und a der öffentliche Schlüssel fertiggestellt.

Die Verschlüsselung kann damit über die Formel
y = xa mod n
erfolgen.

Wir verschlüsseln den Text "KRYPTOGRAFIE" - dazu wandeln wir die Buchstaben in Zahlen um und verwenden dafür den international üblichen ASCII-Code. Wir fassen jeweils 6 Buchstaben zu einer Gruppe zusammen und erhalten 12-stellige Zahlen.

K R Y P T O
75 82 89 80 84 79
G R A F I E
71 82 65 70 73 69

Wir verwenden den DERIVE-Befehl: POWER_MOD(x,a,n) - Resultat von xa mod n.

Verschluesselung

Entschlüsselung:

Zuerst brauchen wir den geheimen Schlüssel - passend zum öffentlichen Schlüssel a, n.

Wir wählen den geheimen Schlüssel b so, dass das Produkt a . b kongruent 1 bezüglich des Modulus m ist. Dies ist gleichbedeutend mit b = a-1 mod m. Dafür verwenden wir den Befehl INVERSE_MOD(x,a).

b erzeugen

Anschließend kann die Entschlüsselung durchgeführt werden - analog zur Verschlüsselung, aber mit Hilfe des geheimen Schlüssels!

Entschluesselung

Die Entschlüsselung ergibt wieder die ASCII-Codes der Buchstaben von "KRYPTOGRAFIE" (wie bei der Verschlüsselung in 6-er-Blöcken geordnet).

 

[ Schliessen ]