- Festlegen der Eckpunkte (gleich in einer Zeile): [a:[-5,-2], b:[6,-1], c:[2,7]]
- Bestimmung der beiden Streckensymmetralen auf die Seiten ab und bc. Zuerst werden die Mittelpunkte der Seiten berechnet: [mab:(a+b)/2, mbc:(b+c)/2]
- Anschließend werden die beiden Streckensymmetralen aufgestellt:
stab:[x,y].(b-a) = mab.(b-a) und
stbc:[x,y].(c-b) = mbc.(c-b)
- Wir suchen den Umkreismittelpunkt als Lösung des Gleichungssystems:
um:linsolve([stbc,stab], [x, y])
- Anschließend berechnen wir den Umkreisradius:
rum:absv2(um-a) (wobei der Befehl absv2 zuerst definiert werden muss!)
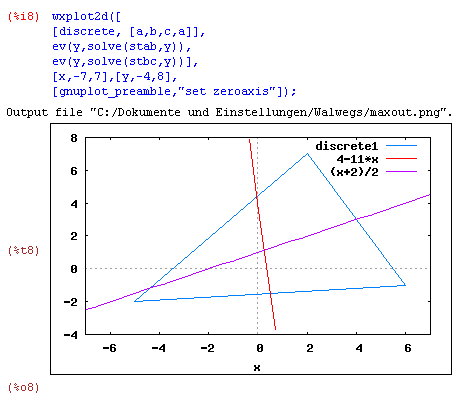
Zeichnung, 2D-Plot:
- Vektor [a,b,c,a] = Punkte a, b, c und d zu einem Streckenzug verbinden und plotten.
- Plot der beiden Streckensymmetralen stab und stbc.
|