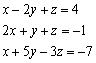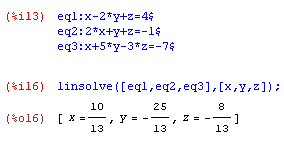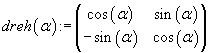Maxima

Matrizen (und Vektoren)

Ein rechteckiges Tableau von mathematischen Ausdrücken - im einfachsten Fall sind das Zahlen - nennt man eine Matrix. Sie wird gekennzeichnet durch die Anzahl ihrer Zeilen und Spalten (zB. 4 x 3 ... 4 Zeilen zu 3 Elementen, entspricht 4 Vektoren mit je 3 Elementen).
Eine Matrix kann damit in MAXIMA als Vektor von Vektoren mit gleicher Dimension interpretiert werden. Umgekehrt können damit auch Vektoren als Matrizen aufgefasst werden (1 x 3 ... Zeilenvektor, 3 x 1 ... Spaltenvektor).

Hinweis - manchmal unterscheidet sich die Form der Daten von der für die gewünschte Aktion notwendigen Vorlage, daher braucht man die Umwandlung von Matrizen in Listen (bzw. Listen in Matrizen) - über den Link kommt man zu selbstdefinierbaren Funktionen.

Eingabe von Matrizen:

Eingabe über das Menü: ALGEBRA - MATRIX EINGEBEN, Dialogfenster: Definition der Dimension der Matrix und Eingabe der Elemente.
Eingabe direkt über die Tastatur über den Befehl matrix()
Beispiel: A:matrix([3,2,1],[1,2,4],[1,0,-1])

Matrizenbefehle
Beispiel 1 - Spalten- und Reihenoperationen auf Matrizen
Beispiel 2 - lineare Gleichungssysteme
Beispiel 3 - Drehmatrizen
Übung 1: Hauptachsentransformation
Übung 2: Symmetrische Verschlüsselung

Matrizenbefehle:

`A[i], A[i,j]`	A[i] liefert eine Liste mit den Elementen der i-ten Zeile der Matrix A, A[i,j] liefert das ij-te Element (i-te Zeile, j-te Spalte).
`row(A,1), col(A,1)`	Zugriff auf eine (hier die erste) Reihe/Spalte von A
`rowswap(A,i,j)`	Vertauscht die Reihen i und j der Matrix A
`rowop(A,i,j,factor)`	Reihenoperation auf einer Matrix: A[i] wird neu gebildet aus `A[i]-factor*A[j] rowop(A,i,i,1-c) multipliziert eine Reihe mit dem Faktor c`
*`+, -, , /`**	Matrizenaddition, -subtraktion etc. (Elementweise)
*`Ak`**	Multiplikation der Matrix A mit einem Skalar k. Ein Skalar ist zum Unterschied von einem Vektor und einer Matrix eine Größe, die nur aus einer einzigen Komponente - im Allgemeinen einer reellen Zahl - besteht
`A.B`	Multiplikation von Matrizen (Produktmatrix). Zwei Matrizen können nur multipliziert werden, wenn die Spaltenanzahl der linken Matrix mit der Zeilenanzahl der rechten übereinstimmt! A (5 x 2) * B (2 x 3) ergibt eine Matrix C (5 x 3) - allgemein: A(i x j) * B(j x k) = C(i x k). Achtung: MAXIMA kennt auch komponentenweise Multiplikation bzw. Division - Eingabe mit `*, /`.
`matrix_size(A)`	Gibt die Anzahl der Reihen und Spalten der Matrix A zurück.
`rank(A)`	Rang einer Matrix - Anzahl der linear unabhängigen Zeilen
`transpose(A)`	Transponierte Matrix von A
`invert(A)` oder `A^^-1`	Inverse Matrix von A
`determinant(A)`	Determinante von A
`diagmatrix(n,x)`	Erzeugt eine nxn Diagonalmatrix (alle Diagonalelemente werden auf "x" gesetzt, alle anderen Elemente auf 0).
`ident(n)`	Erzeugt eine nxn Einheitsmatrix (alle Diagonalelemente werden auf "1" gesetzt, alle anderen Elemente auf 0).
`zeromatrix(n,m)`	Erzeugt eine nxm Nullmatrix.
`triangularize(A)`	Erzeugt die ober Dreiecksform der Matrix A (entsteht durch Gauß'sche Elimination) - unter der Diagonalen stehen nur mehr Nullen!.
`gramschmidt(A,i)`	Gram-Schmidt Orthogonalisierung von A.
`addcol(), addrow()`	Spalte bzw. Reihe hinzufügen Beispiel: addcol(A,[1,5,7]) fügt die Spalte [1,5,7] zur Matrix A hinzu.
`submatrix(i1,...,im,A) submatrix(A,j1,...,jn)`	Entfernt die Zeilen i1, ..., im aus der Matrix A bzw. entfernt die Spalten j1, ..., jn.
`coefmatrix([Gleich.],[Variable])`	Erzeugt aus den gegebenen Gleichungen die Koeffizientenmatrix mit den angegebenen Variablen.
`augcoefmatrix([Gleich.],[Var.])`	Ergänzt die Koeffizientenmatrix eines Systems von linearen Gleichungen um die konstanten Glieder als zusätzliche Spalte
`charpoly(A,v)`	Charakteristisches Polynom der quadratischen Matrix A mit der Variable v
`eigenvalues(A)`	liefert die Eigenwerte der quadratischen Matrix A - zuerst kommen die Eigenwerte, dann die Häufigkeit des Vorkommens
`eigenvectors(A)`	liefert die Eigenwerte der quadratischen Matrix A - zuerst kommen die Eigenwerte, dann die dazugehörigen Eigenvektoren

Hinweis - Matrizen (wie alle Listenobjekte) lassen sich nicht durch eine einfache Variablenzuordnung kopieren, man benötigt dafür einen eigenen Befehl! (copymatrix(A)). Die Zuordnung A:m1 erzeugt nur eine Referenz auf die Matrix m1, aber keine neue Matrix A!

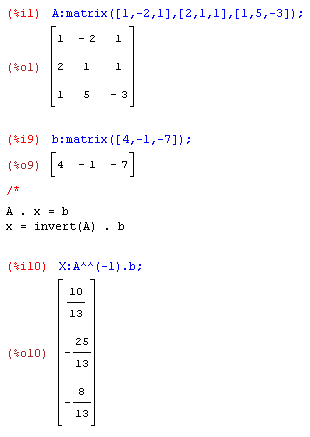
Beispiel 1 - Spalten- und Reihenoperationen auf Matrizen:

Erzeugen Sie die Matrix A mit den Zeilenvektoren [1,-2,1], [2,1,1] und [1,5,-3]. Anschließend werden Spalten vertauscht und Reihenoperationen durchgeführt.

Operationen auf Reihen

Beispiel 2 - lösen von linearen Gleichungssystemen:

Lösen Sie das folgende Gleichungssystem mit Hilfe von Matrizen, kontrollieren Sie mit LINSOLVE.

Gleichungssystem

Gleichungssystem1

Determinante ungleich 0 bedeutet, das Gleichungssystem ist eindeutig lösbar!

Linsolve

Gleichungssystem2

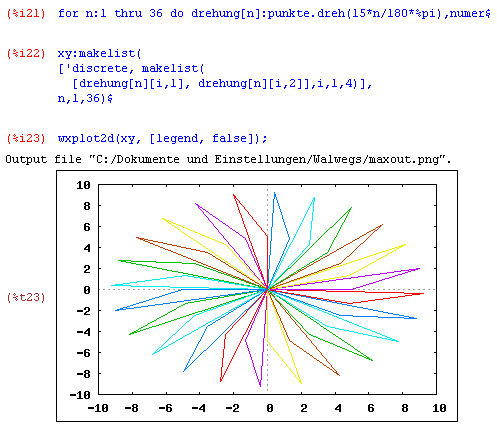
Beispiel 3 - Drehmatrizen:

Eine Drehung im Zweidimensionalen kann immer mit Hilfe einer Drehmatrix beschrieben werden. Diese wird mit den Vektoren multipliziert, durch die die Figur beschrieben ist. Eine Drehmatrix ist stets von der Form:
Formel

Durch Multiplikation der Matrix, die eine geometrische Figur definiert (zB. ein Dreieck), mit der Drehmatrix entsteht die gedrehte Figur.

Drehmatrix

Plot

Übung 1 - Hauptachsentransformation:

Gegeben ist ein Kegelschnitt durch die folgende "Quadrik"

Stellen Sie fest, wie die Normalform der Quadrik lautet - plotten Sie diese und berechnen Sie die Hauptachsenlängen!

MAXIMA-Datei

Übung 2 - Symmetrische Verschlüsselung:

Symmetrische Verschlüsselung mit Hilfe von Matrizenoperationen: der Text "Das ist ein Geheimtext" soll verschlüsselt werden.
Vorgangsweise:

Umwandlung des STRINGs in eine LISTE (Befehl: charlist(String), anschließend Umwandlung der Zeichen mit Hilfe der ASCII-Codes in Zahlen
MAXIMA-Befehl: cint(Character)
Anordnung des Buchstabenvektors in eine Matrix mit fixierter Spaltenzahl (zB. 4-spaltig)
Falls nötig, wird der Geheimtext um Leerzeichen ergänzt, um die Matrix aufzufüllen.
Verschlüsselung des codierten Textes mit Hilfe einer Schlüsselmatrix (quadratisch, nichtsingulär = Determinante ungleich 0), im Falle einer 4-spaltigen Ausgangsmatrix also eine nichtsinguläre 4x4-Matrix.
geheim := klar . schluesselmatrix
Rückverwandlung mit klar := geheim . schluesselmatrix^^-1 (inverse Matrix)
ascii(Zahl) verwandelt die Zahlen wieder in Buchstaben, simplode(Liste) macht aus der Liste den Ausgangstext (einen String).

MAXIMA-Datei