Ableiten mit dem Computer

Die Ableitung einer Funktion kannst du auch mit dem Computer bestimmen. Hier siehst du, wie das mit GeoGebra und dem Computeralgebrasystem Derive geht.

Derive In Derive erhältst du die Ableitung der Funktion f(x) = 3 x2 mit folgenden Befehlen. f(x) := 3 x^2 DIF( f(x), x ) Das Ergebnis ist 6x. Im 2D-Plot Fenster kannst du Funktion und Ableitung zeichnen lassen.

GeoGebra In GeoGebra bekommst du die Ableitung von f(x) = 3 x2 so: f(x) = 3 x^2 Ableitung[ f ] Hier werden die Funktion f(x) = 3 x2 und ihre Ableitung f'(x) = 6x gleich automatisch gezeichnet.

Schrittweises Ableiten mit Derive

Mit dem Computeralgebrasystem Derive können (ab Version 6) auch die verwendeten Ableitungsregeln schrittweise angezeigt werden. Dazu wählt man im Menü "Simplify" den Punkt "Display Step". Für das Beispiel von oben mit f(x):=3 x^2 und DIF(f(x), x) siehst du die Ableitungsregeln in folgenden Screenshot von Derive: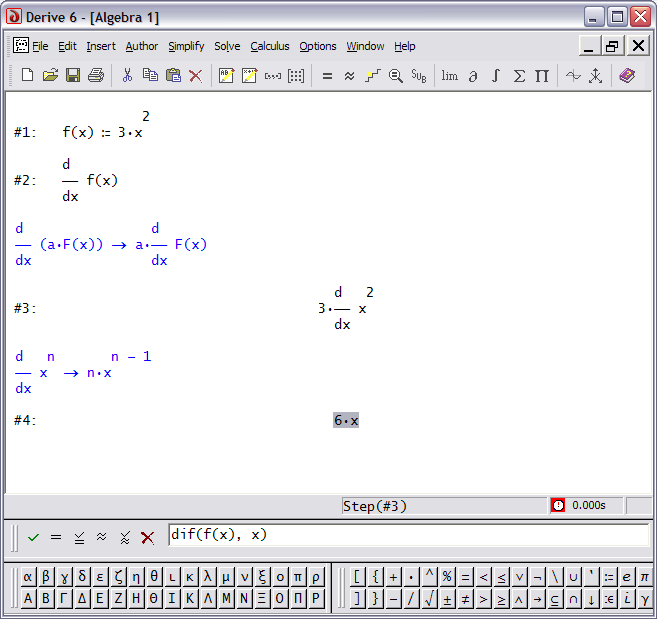
      

Probiere dieses schrittweise Vereinfachen für kompliziertere Funktionen aus und versuche alle auftretenden Ableitungsregeln zu erkennen!

Grenzwertberechnung mit Derive

Mit dem Computeralgebrasystem Derive kann man auch den Grenzwert eines Differentialquotienten berechnen lassen. Damit kann man die Ableitung unseres einfachen Beispiels auch so berechnen:

Als Ergebnis liefert Derive auch hier 6x.