Funktionen beschreiben Abhängigkeiten   

Funktionen beschreiben Abhängigkeiten zwischen Größen.

Wenn eine Größe (z.B. der Flächeninhalt eines Quadrats) von einer anderen Größe (z.B. die Seitenlänge) abhängt, so kann diese Abhängigkeit durch eine Funktion beschrieben werden. Bezeichnen wir den Flächeninhalt mit F und die Seitenlänge mit a, so ist F = a². Das ist zunächst nur eine "Formel".

Motiviert durch diese Formel können wir eine Funktion definieren:

• Zuordnungsvorschrift (Termdarstellung):
  
  F(a) = a².
  Das bedeutet: Der Flächeninhalt wird gewonnen, indem die Seitenlänge quadriert wird.
   
• Angabe von Definitions- und Zielmenge:

  Definitionsmenge = Menge R⁺ aller positiven reellen Zahlen
  Zielmenge = Menge R aller reellen Zahlen

  Wir können das in Kurzform als
  
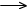  F : R⁺ R
  anschreiben. Das bedeutet: Jeder positiven reellen Zahl (der Seitenlänge) wird eine reelle Zahl (der Flächeninhalt) zugeordnet.

Beachte, dass der Begriff der "Funktion" schärfer als jener der "Formel" ist!

Der Name der abhängigen Größe wird oft (wie auch im obigen Beispiel) als Name der Funktion verwendet. Durch die Schreibweise F(a) = a² wird ausgedrückt, wie F von a abhängt.

Achtung: Der Schritt von einer Formel zu einer Funktion ist nicht immer eindeutig. So könnte man durchaus auch bei der Quadratfläche den Grenzfall 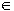a = 0 zulassen und als Definitionsmenge R⁺₀ = { x R | x 0} wählen. Als Zielmenge könnte man statt R genauso gut R⁺₀ (oder, wenn die Definitionsmenge R⁺ ist, ebenfalls R⁺) angeben.