Flächeninhaltsfunktion
|
Die Berechnung des bestimmten Integrals als Grenzwert von Unter- und Obersumme ist aufwändig und langwierig. Wir wollen daher nach einer Möglichkeit suchen, wie man das bestimmte Integral einer Funktion einfacher berechnen kann. Im rechten Fenster ist das bestimmte Integral von f(x) = x2 in einem Intervall [a, b] zu sehen. Bei der Intervallgrenze b ist zusätzlich der Wert des bestimmten Integrals F von der x-Achse aus abgetragen.
|
|
Flächeninhaltsfunktion und bestimmtes Integral
Mit Hilfe einer
Flächeninhaltsfunktion F(x)
zur gegebenen Funktion f können wir den Wert des bestimmten Integrals im
Intervall
[a, b] sehr einfach berechnen: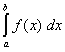 =
F(b) - F(a) =
F(b) - F(a)
|
Ergebnis
Wir wissen jetzt, dass wir mit einer Flächeninhaltsfunktion ganz einfach das bestimmte Integral berechnen können.Die Frage ist nun: Wie bekommt man so eine Flächeninhaltsfunktion?