Dreieck 2: Thaleskreis

Thales von Milet war ein wichtiger griechischer Mathematiker. Er zählt zu den „Sieben Weisen“ des antiken Griechenland und lebte um 600 vor Christus in Milet, einem Ort an der Westküste Kleinasiens.
Quelle Bild: www.anderegg-web.ch/ phil/thales-de-milet.jpg

Thales hat einen wichtigen Satz für rechtwinkelige Dreiecke entdeckt: den Satz vom Thales. Kannst du dich noch vom Unterricht her daran erinnern?

Thales hat herausgefunden: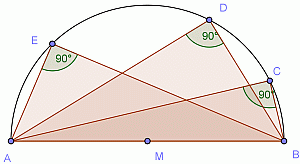

Liegt eine Ecke eines Dreiecks auf dem Halbkreis über der gegenüber liegenden Seite, so hat der entsprechende Winkel eine Größe von 90°.

Aber: Warum ist das so?

Warum sind alle Winkel über einem Halbkreis (siehe Abbildung) rechte Winkel? Warum funktioniert das in jedem beliebigen Halbkreis?

Thales von Milet wird nicht nur die Entdeckung dieser Eigenschaft – des Satzes von Thales - sondern auch deren Beweis zugeschrieben. Ein Beweis ist nicht die Beschreibung einer Eigenschaft, ein Beweis zeigt die Allgemeingültigkeit eines Satzes durch logisches Argumentieren, Folgern und Schließen.

Sorry, the GeoGebra Applet could not be started. Please make sure that Java 1.4.2 (or later) is installed and activated. (click here to install Java now)

Vielleicht ist Thales auf seinen Lehrsatz gekommen, indem er sich die Diagonalen des Rechtecks genau angeschaut hat. Überlege: Welche Eigenschaften haben die Diagonalen eines Rechtecks und wie folgt dann der Satz von Thales? Verwende das links stehende dynamische Arbeitsblatt und führe folgende Aufgaben aus: Fasse mit der Maus den Punkt C an und ziehe ihn mit gedrückter linker Maustaste, beobachte dabei die Größe der Winkel - vor allem des Winkels γ. Der Punkt C bewegt sich nur auf der Kreislinie. Wenn du den Punkt B ziehst kannst du auch den Radius des Kreises verändern. Wie ist in diesem dynamischen Arbeitsblatt der Satz von Thales veranschaulicht?

• Diese Beweisidee wird in diesem Applet verwendet - der Beweis ist aber nicht zu Ende durchgeführt. Notiere im Heft die Weiterführung des Beweises.
   
• Nun bist du schon fast ein Profi fürs Beweisen! Da wird dir dieses Applet zum Beweis des Satzes von Thales sicher keine Schwierigkeiten machen! Führe die Anweisungen des Applets aus und notiere die Ergebnisse folgender Punkte aus dem Applet im Heft:
   
  • Von der ersten Seite: Formuliere deine Beobachtungen in Form eines Satzes.
  • Von der zweiten Seite: Beachte, dass du keine Spezialfälle sondern allgemein gültige Begründungen aufschreiben sollst. Mache dafür eine Skizze, in der du die Winkel auch schon allgemein mit α, β, ... bezeichnest. Beachte, welche Winkel gleich groß sind!
     
    1. Begründe, warum das Dreieck ABC von der Strecke CU in zwei gleichschenklige Dreiecke unterteilt wird. Welche Seiten sind dabei gleich lang?
    2. Wo treten die Winkel α und β nochmals auf? Wie setzt sich der Winkel γ zusammen?
    3. Berechne nun die Winkelsumme im Dreieck ABC. Wie lässt sich daraus mit Hilfe von Aufgabe 2 der Winkel γ berechnen?
  
  Kontrolliere nochmals, ob du wirklich allgemein gültige Begründungen angegeben hast und ob dein Beweis wirklich schlüssig ist. Trage diesen Beweis nun deinen Klassenkameraden vor.
  Sei vorsichtig, sie werden Fragen stellen, wenn sie sich nicht auskennen. Diese musst du als großer Thales beantworten können.