Faktorisierung

Der Hintergrund der ausführlichen Beschäftigung mit den Restklassen, Primzahlen usw. ist die grundlegende Idee der modernen Kryptographie, für eine asymmetrische Verschlüsselung (Public-Key-Verfahren) Einwegfunktionen mit Falltür (engl. trapdoor one-way) zu verwenden. Klingt kompliziert - ist aber recht einfach.

• Asymmetrische Verschlüsselung - für einen sicheren Austausch der Schlüssel müssen sich Sender und Empfänger einer verschlüsselten Nachricht nicht mehr vorher physisch begegnen.
• Public Key Verfahren - Verfahren mit einem Schlüsselpaar. Der Öffentliche Schlüssel (für die Verschlüsselung) wird ergänzt durch einen privaten Schlüssel (für die Entschlüsselung).
• Einwegfunktion - eine effizient zu berechnende Funktion, deren Umkehrung jedoch nur mit extrem hohem Rechenaufwand (in der Praxis in einer für Menschen nicht mehr vertretbaren Zeit) zu berechnen ist.
• Falltür - Zusatzinformation, die aus einer Einwegfunktion eine umkehrbare Funktion macht.

Nachdem die grundsätzliche Möglichkeit formuliert wurde, mit Hilfe solcher Einwegfunktionen mit Falltür ein asymmetrisches Verschlüsselungsverfahren zu betreiben, begann die Suche nach geeigneten Funktionen. Die bekannteste derartige Funktion ist die Primfaktorenzerlegung. Wie wir bereits bei den Primzahlen herausgefunden haben, lässt sich zwar jede Zahl in ihre Primfaktoren zerlegen, für die Zerlegung existiert aber kein rascher Algorithmus. Wenn daher die Zahlen groß genug angesetzt werden, ist die Faktorisierung ein sehr langwieriger Prozess - bei sehr großen Zahlen (mehrere 100 Dezimalstellen) in vertretbarer Zeit (zig Jahren! - selbst wenn alle Computer der Welt gleichzeitig daran arbeiten würden) faktisch unmöglich.
Der Satz von Euler bietet zusammen mit dem erweiterten euklidischen Algorithmus aber die Möglichkeit, in die Primfaktorenzerlegung (über die Kenntnis der Faktoren) eine effiziente Falltür einzubauen.

Faktorisierung von (relativ kleinen) Zahlen mit Hilfe von DERIVE

• FACTOR(m) - Zerlegung einer Zahl in ihre Primfaktoren

Beispiel:
Zerlege die Zahlen 1875 und 24474565452 in ihre Primfaktoren.

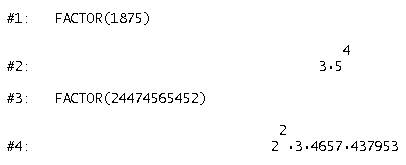
Was bei kleinen Zahlen noch so selbstverständlich aussieht, ändert sich drastisch bei einer Erhöhung der zu untersuchenden Zahl. Bei der Faktorisierung von 2²⁹⁹ - 1 ist es auch bei schnellen Rechnern (ein moderner PC schafft immerhin mehrere Milliarden Rechenprozesse pro Sekunde!) aus mit der raschen Faktorisierung. Während DERIVE sehr rasch feststellen kann, dass es sich um keine Primzahl handelt, ist die Ermitttlung der Primfaktoren eine langwierige Sache.