Restklassen - Kongruenzklassen

Inhalt:

• Einführung - Problemstellungen aus Alltag und Informatik
• Definition des Restklassenbegriffs
• modulares Addieren, Subtrahieren und Multiplizieren
• modulare Division
• modulares Potenzieren

---

Einführung

Die Ganzzahldivision liefert ein Ergebnis und einen Rest. Bei manchen Problemen interessieren wir uns ausschließlich für den Rest!

Problemstellung aus dem Alltag:

• es ist 10.00 Uhr (vormittag) und wir wollen wissen, wie spät es in 50, 70, 125 Stunden ist!

Die Lösung des Problems liegt darin, die Zeiten auf den 24-Stunden-Rhythmus des Tages umzulegen. Man könnte wie folgt rechnen:

(10 + 50) mod 24 = 60 mod 24 = 12

(10 + 70) mod 24 = 80 mod 24 = 8

(10 + 125) mod 24 = 135 mod 24 = 15

Antworten: es wäre nach 50 Stunden 12.00 Uhr, nach 70 Stunden 8.00 Uhr, nach 125 Stunden 15.00.

Problemstellung aus der Informatik:

• die Farbe eines Textes soll sich regelmäßig ändern
• wir haben eine begrenzte Anzahl Farben zur Verfügung (z.B. 16)
• die Änderung soll bis zu einem willkührlich gesetzten Abbruch erfolgen

Die Zahl der Änderungen wird in einer Zahl angegeben - diese wird immer höher und höher - muss aber irgendwie auf den Zahlenbereich 0 .. 15 (16 Möglichkeiten) heruntertransformiert werden.
Die Lösung bietet die MODULO-Rechnung (der Rest der Ganzzahldivision).

• i ... Zähler der Veränderungen, läuft als positive ganze Zahl von 0 bis X (wobei X beliebig groß werden kann).
• r = mod(i, 16) liefert den Rest der Ganzzahldivision durch 16, r wird bei jeder Veränderung um 1 erhöht, springt aber, sobald 16 erreicht ist, wieder auf 0 und beginnt von vorne.
• Ergebnis: 0, 1, 2, 3, 4, 5, ... , 14, 15, 0, 1, 2, ... , 15, 0, 1, 2, ...

Definition des Restklassenbegriffs

Alle Zahlen, die bei Division durch 16 denselben Rest ergeben, nennt man eine Restklasse MODULO 16.

Beispiel:

• Restklasse von 1 MODULO 16 = {-31, -15, 1, 17, 33, 49, ... }
• Restklasse von 5 MODULO 24 = {-19, 5, 29, 53, 77, 101, ... }

In unserem Beispiel heißt das:

Restklasse 1 MODULO 16 ... Repräsentant 1

Restklasse 5 MODULO 24 ... Repräsentant 5

Die Restklassen bilden algebraische Strukturen und erfüllen teils weitgehende mathematische Gesetzmäßigkeiten.

Übung: Berechne mit Hilfe eines geeigneten Computeralgebrasystems / Taschenrechners folgende Gleichungen: x = 250 mod 36 5 = x mod 8 5 = 11 mod x Beachte, ob es eindeutige Lösungen gibt! Die vorgestellte Lösung wurde mit DERIVE erstellt.

modulares Addieren, Subtrahieren und Multiplizieren

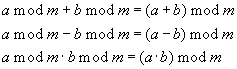
Übung: Überprüfe: 281 mod 29 + 355 mod 29 = 636 mod 29 389 mod 39 + 455 mod 39 = (389 + 455) mod 39 503 * 222 mod 5 = 503 mod 5 * 222 mod 5 Die vorgestellte Lösung wurde mit DERIVE erstellt.

modulares Dividieren

Division ist die inverse Operation der Multiplikation. Jede Division kann daher beantwortet werden, indem man die "fehlende " Zahl bei der zugehörigen Multiplikation findet.

Beispiel:

9 * 5 = 13 mod 16	9 * 5 = 45, 45 DIV 16 = 2, Rest 13
daraus folgt
9 = 13 / 5 mod 16	wobei das "Dividiert-Zeichen" hier etwas anders interpretiert werden muss als gewohnt. Die Division 13 / 5 hat ausnahmsweise gar nichts mit einem Bruch zu tun!
Wir wollen nun versuchen, wie man auf die Zahl 9 als Ergebnis kommen kann.
x = 13 / 5 mod 16	Wir wollen x berechnen und multiplizieren beide Seiten mit 5.
5x = 13 mod 16	Wir suchen x, indem wir die Reste 0 .. 15 für x einsetzen und ausprobieren, bei welchem Rest die Gleichung erfüllt ist.
5 * 1 = 5 mod 16 5 * 2 = 10 mod 16 5 * 3 = 15 mod 16 5 * 4 = 4 mod 16 5 * 5 = 9 mod 16 5 * 6 = 14 mod 16 5 * 7 = 3 mod 16 5 * 8 = 8 mod 16 5 * 9 = 13 mod 16	Leider ist dieses Verfahren nur für einen kleinen modulus geeignet. Für höhere Zahlen braucht man ein besseres Verfahren. Dieses kann mit Hilfe des Erweiterten Euklidischen Algorithmus durchgeführt werden.

Übung: Berechne x: x = 8 / 7 mod 12 x = 8 / 7 mod 20 x = 5 / 11 mod 13

modulares Potenzieren

modulares Potenzieren kann auf wiederholte Multiplikation reduziert werden.

Beispiel: 7^4 mod 12 = ?

Eine - scheinbar einfache - Methode lautet: berechne 7^4 = und berechne anschließend 2401 mod 12 = 1. Diese Methode funktioniert zwar sehr gut bei kleineren Zahlen, stößt aber bei sehr hohen Zahlen an Grenzen.

Eine zweite Möglichkeit: 7^4 = 7^2 * 7^2 - wir verwenden die Regeln des modularen Multiplizierens!

7^4 = 7^2 * 7^2 = 49 * 49

49 * 49 mod 12 = 49 mod 12 * 49 mod 12

49 mod 12 = 1

7^4 mod 12 = 7^2 mod 12 * 7^2 mod 12 = 1 * 1 = 1

Beispiel: 82^17 mod 20 = ?

82^17 mod 20 = 2^17 mod 20

2^17 mod 20 = (2^4)^4 * 2 mod 20

16^4 * 2 mod 20 = (-4)^4 * 2 mod 20

16^2 * 2 mod 20 = (-4)^2 * 2 mod 20

16 * 2 mod 20 = 32 mod 20 = 12

Die Lösung lautet 12.

Übung: 54^16 mod 55 = 2^269 mod 19 = 3^333 mod 15 = Überprüfe mit Hilfe eines Computeralgebrasystems deine Berechnungen!