Maxima

Aufgabenstellung: Die lineare Gleichung a*x + b = c soll nach x aufgelöst werden. MAXIMA lässt uns dafür 2 Möglichkeiten offen - wir können die Gleichung mit Hilfe von Äquivalenzumformungen lösen oder mit Hilfe des eingebauten Lösungsbefehls SOLVE arbeiten.

ad 1) Äquivalenzumformungen

ad 2) SOLVE-Befehl

Der SOLVE-Befehl verlangt nach der zu lösenden Gleichung und der Variablen (den Variablen), nach denen die Gleichung aufgelöst werden soll!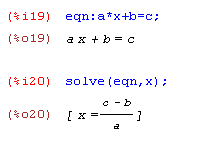

Das erste Argument von SOLVE ist die zu lösenden Gleichung. Falls das Argument keine Gleichung ist, wird das Argument zu einer Gleichung gemacht, indem es gleich Null gesetzt wird. Das zweite Argument ist die Variable, nach der gelöst werden soll.

• SOLVE(u, v) - gibt als Ergebnis eine Liste, deren einzelne Glieder Gleichungen sind (ähnlich der Angabe), zurück.
• ALGSYS([u], [v]) - der übergeordnete Lösungsbefehl von MAXIMA greift auf SOLVE zurück, wenn algebraisch eindeutig zu berechnenden Lösungen existieren mit dem Vorteil, dass hier zusätzliche Regeln wie REALONLY berücksichtigt werden, und greift auf numerische Verfahren zurück, wenn keine eindeutigen Lösungen möglich sind.

Bei Aufruf über das Menü öffnet sich folgender Dialog:

Die Menge, über der der SOLVE-Befehl von MAXIMA arbeitet, lässt sich nicht direkt beeinflussen. Einschränkungen über ASSUME etc. werden hier ignoriert. Über den Befehl algsys können aber Einschränkungen vorgenommen werden, indem die Variable realonly gesetzt wird.

Beispiel:

Löse folgende Gleichung zuerst in der Grundmenge C, anschließend nur für reelle Zahlen: x³ - 4x² + 6x - 4 = 0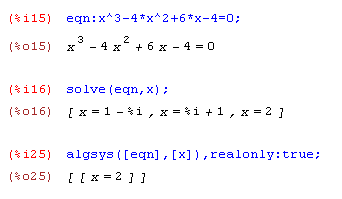

Nicht alle Gleichungen lassen sich exakt lösen. Bereits Polynomgleichungen höherer Ordnung, aber auch div. trigonometrische Gleichungen, Exponentialgleichungen etc. lassen sich nur numerisch lösen.
MAXIMA bietet hierfür mehrere Möglichkeiten, entweder im Menü

• GLEICHUNGEN - NUMERISCH LÖSEN (der Befehl find_root
  (numerische Berechnung der Nullstellen einer Funktion unter Angabe eines Suchintervalls, Achtung: keine Gleichung als Eingabe möglich!) auszuwählen, oder die Befehle
• allroots bzw. realroots für Polynome oder aber den übergeordneten Befehl
• algsys (der auch für Gleichungssysteme genutzt wird)

Wie kann man auf Lösungen, die mit SOLVE berechnet wurden, zugreifen. Einige Hinweise dazu finden Sie im Kapitel zu Gleichungssystemen unter: c_gleich02.htm#solve.

Eine weitere Möglichkeit, einfacher auf Lösungen zuzugreifen, ist die Definition einer eigenen Funktion - wir nennen sie in Anlehnung an DERIVE "solutions()" -, die als Eingabe ein Polynom poly erwartet (dieses wird anschließend in eine Gleichung poly = 0 verwandelt) und die Ergebnisse direkt als Liste ausgibt. Wir verwenden dazu die LAMBDA-Funktion von MAXIMA.