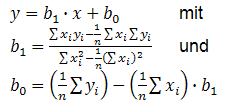Maxima

Lineare Regression

Inhalt

Methode der kleinsten Quadrate

Maxima kennt leider im Standardbefehlssatz keine Funktionen für Regressionsgeraden und -kurven. Die hervorragende Programmierbarkeit des Systems lässt aber sehr leicht Ergänzungen zu.

Aufgabe: wir suchen für eine gegebene Punktwolke mit Paaren von Messdaten (xi, yi) ein lineares Modell - also die "beste" Gerade durch die Punktwolke. Dies erfolgt durch Minimierung der Summe der Fehlerquadrate (Abstände der gegebenen Punkte zur Geraden mit Gewichtung). Die Lösung dieser Aufgabenstellung ist eine Regressionsgerade der Form:

Lineare Regression 01

Wir definieren eine Funktion linreg(punktliste,var), die als Ergebnis die rechte Seite der Regressionsgerade in der Variablen var liefert, also b1*var + b0.

linreg(liste,var):=block(
  [anz:0,i:1,lx,ly],
  anz:length(liste),
  lx:makelist(liste[i][1],i,1,anz),
  ly:makelist(liste[i][2],i,1,anz),
  b1:(sum(lx[i]*ly[i],i,1,anz)-
     1/anz*sum(lx[i],i,1,anz)*sum(ly[i],i,1,anz))
     /(sum(lx[i]^2,i,1,anz)-1/anz*(sum(lx[i],i,1,anz))^2),
  b0:1/anz*sum(ly[i],i,1,anz)-1/anz*sum(lx[i],i,1,anz)*b1,
  return(b0+b1*var)
)$

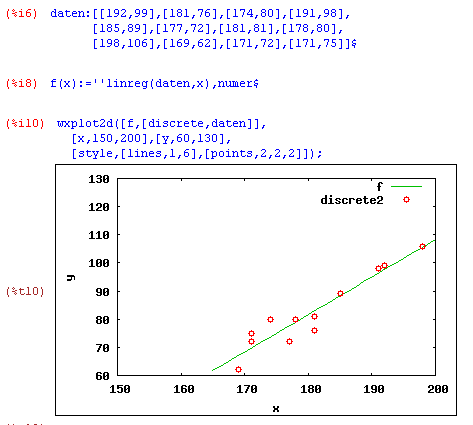
Anschließend wird die Funktion mit Probedaten getestet. Wir nehmen 12 Zahlenpaare (Größe und Gewicht von Probanden) und sehen nach, ob zwischen der Körpergröße und dem Körpergewicht der getesteten Personen ein linearer Zusammenhang feststellbar ist.

Lineare Regression 02

 

MAXIMA-Datei
zurueck

Median-Median-Gerade

Die Median-Median-Linie ist eine einfache, robuste Alternative zu der am häufigsten verwendeten Methode der kleinsten Quadrate. Die Methode reagiert vor allem weit weniger empfindlich auf Ausreißer im Datenmaterial.

Ziel der Median-Median-Linie ist:

  • Teile die Daten in drei Bereiche mit einer gleichen Anzahl von Datenpunkten
  • Definiere einen Summationspunkt für jeden Bereich
  • Nutze die drei Summationspunkte, um die Median-Median-Linie zu definieren

Vorgangsweise
(nach dem Algorithmus, der in den TI-Taschenrechnern verwendet wird):

1) Der Algorithmus zerlegt die Liste in drei gleiche Bereiche, ohne dabei Gruppen mit gleichen x-Werten aufzubrechen. In solchen Fällen werden mindestens 1/3 der Punkte in die linke bzw. rechte Gruppe aufgenommen. Der überbleibende Rest wird in die Mittelgruppe gestellt, im Idealfall ebenfalls ein Drittel. Man fällt also zuerst die äußeren Gruppen und die übrigbleibenden Punkte werden zur Mittelgruppe. Wenn diese leer ist, gibt es einen Fehler.

Der Grund, warum gleiche x-Werte nicht getrennt werden, ist abzusichern, dass es die gleichen Ergebnisse unabhängig von der Sortierung der Daten in der Originalliste gibt. Ohne diese Einschränkung würden je nach Sortierung möglicherweise unterschiedliche Ergebnisse auftreten.

2) Ein Summationspunkt ist einfach der Median aller x- und y-Werte in diesem Bereich. Wir bezeichnen diese Summationspunkte mit (x1,y1), (x2,y2) und (x3,y3).

3) Die Median-Median-Linie geht parallel zur Linie durch die Punkte P1(x1,y1) und P3(x3,y3)
        a=(y3-y1)/(x3-x1)
und 1/3 der Distanz zwischen der Linie durch die zwei Summationspunkte und eine parallele Linie durch den zweiten Summationspunkt (x2,y2).
        b=(y1+y2+y3-a*(x1+x2+x3))/3.

 

MAXIMA-Datei

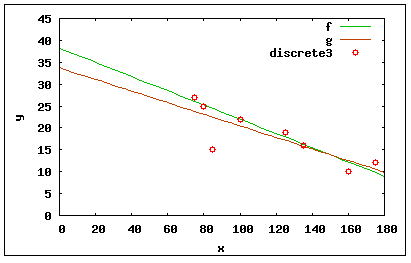
Lineare Regression 01

Der Unterschied zwischen den beiden Regressions-Varianten (kleinste Quadrate - Median-Median) wird in der nebenstehenden Graphik offensichtlich.

f, grün ... Median-Median
g, rot ... kleinste Quadrate
zurueck

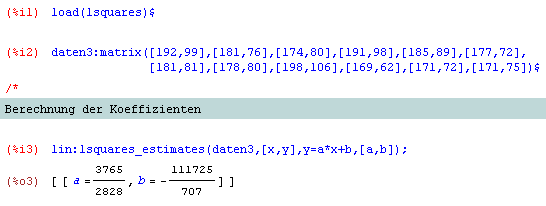
Lösung mit dem Maxima-Paket: lsquares

Eine weitere Möglichkeit, auf Regressionslinien in Maxima zuzugreifen, bietet das mitgelieferte Paket lsquares (least squares - kleinste Quadrate). Eine genaue Beschreibung der enthaltenen Funktionen findet man im Bereich nonlineare Regressionen.

Lineare Regression 04

MAXIMA-Datei
zurueck
Links:

© PH-NOe, letzte Änderung am 12. Mai 2008, erstellt von Walter Wegscheider