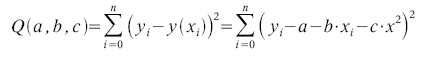Maxima
Nonlineare Regression
Inhalt
- Quadratische Regression - quadreg(daten,var)
- Weitere nonlineare Regressionen über das Paket lsquares
- Beispiele
Quadratische Regression - quadregFür die quadratische Regression sucht man die Funktion Die Berechnung des gewünschten Minimums erfolgt über die partiellen Ableitungen nach den Koeffizienten. Die Lösung des dadurch entstehenden Gleichungssystems in den Koeffizienten a, b und c kann in folgende Maxima-Funktion zusammengefasst werden: |
|||||||||||||||||||||||||||
quadreg(liste,var):=block(
[n:0,i:1,j:1,k:1,lx,ly,lz,a,b,c],
n:length(liste),
lx(k):=1/n*sum(liste[i][1]^k,i,1,n),
ly():=1/n*sum(liste[i][2],i,1,n),
lz(j,k):=1/n*sum(liste[i][1]^j*liste[i][2]^k,i,1,n),
c:((lz(1,1)-lx(1)*ly())/(lx(2)-lx(1)^2)-
(lz(2,1)-lx(2)*ly())/(lx(3)-lx(1)*lx(2)))
/
((lx(3)-lx(1)*lx(2))/(lx(2)-lx(1)^2)-
(lx(4)-lx(2)^2)/(lx(3)-lx(1)*lx(2))),
b:(lz(1,1)-lx(1)*ly())/(lx(2)-lx(1)^2)-
c*(lx(3)-lx(1)*lx(2))/(lx(2)-lx(1)^2),
a:ly()-lx(1)*b-lx(2)*c,
return(a+b*var+c*var^2)
)$
|
|
||||||||||||||||||||||||||
|
Überprüfung der Funktion mit geeignetem Datenmaterial:
|
|||||||||||||||||||||||||||
Regressionen mit dem Maxima-Paket: lsquaresMaxima bietet über ein mitgeliefertes Funktionspaket ebenfalls Möglichkeiten, einfach Regressionslinien zu berechnen - das Paket heißt lsquares. Über load(lsquares) kann (unter anderem) auf folgende Funktionen zugegriffen werden:
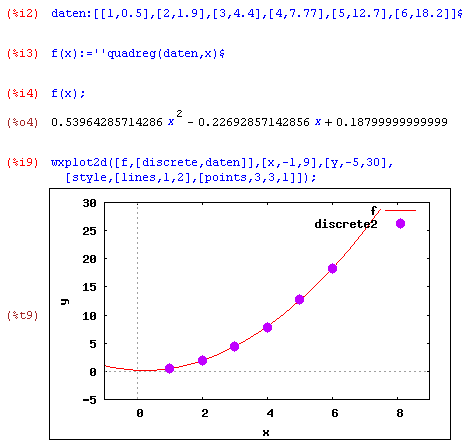
Hinweis - Die Daten müssen in Form einer Matrix vorliegen, wobei jede Zeile die Variablen enthält. Bei einer Funktion in x und y handelt es sich also um eine nx2-Matrix (Schwierigkeit: für einen Plot muss die Matrix in eine Liste umgewandelt werden!) Beispiel:Wir testen das Paket lsquares mit einer kubischen Regression. Eine Funktion des Typs: a*x^3+b*x^2+c*x+d soll an das vorhandene Datenmaterial angepasst werden.
Anschließend fügen wir das Ergebnis der Regression für die Koeffezienten a, b, c und d in die Funktionsgleichung ein und definieren eine kubische Funktion f1(x).
Wir wandeln die Datenmatrix in eine Liste um und plotten die Daten als Scatterplot mit der Regressionskurve f1(x).
|
|||||||||||||||||||||||||||
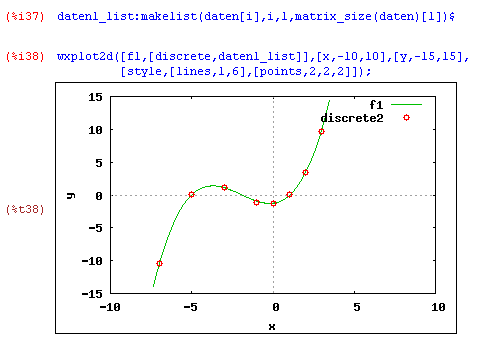
BeispieleParabel (Quadratische Regression):Gegeben sind drei Punkte P(-5,2), Q(-1,3) und R(3,0). Bestimme jene Parabel, die durch die drei Punkte geht.
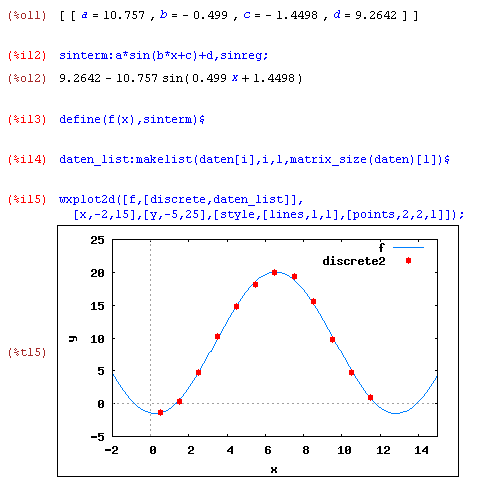
Welches Wetter herrscht in Wien (Sinusregression):Welches Wetter herrscht in Wien? - die Lufttemperatur schwankt täglich und hängt von zahlreichen Einflüssen ab. Untersucht man jedoch den Verlauf der langjährigen Monatsmittelwerte, so lassen sich erstaunliche Gesetzmäßigkeiten erkennen.
Der Plot der Datenpunkte und der mit Hilfe der Regression bestimmten Funktion zeigt den Zusammenhang - bei den monatlichen Durchschnittstemperaturen erhält man (bis auf lokal begründbare Abweichungen) eine Sinuskurve! Die Parameter lassen sich recht leicht auch geographisch begründen: Hinweis - Bei der Sinusregression können die gesuchten Koeffizienten nur über Approximation gefunden werden - Maxima zeigt einige Stufen an, über welche Zwischenwerte vorgegangen wird!
|
|||||||||||||||||||||||||||
Links:
|
|||||||||||||||||||||||||||