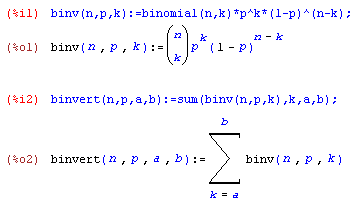Maxima

Wir gehen von einem Zufallsexperiment (Basisexperiment oder auch Bernoulliexperiment) aus. Ein derartiges Experiment hat 2 mögliche Ausgänge:

• A ... das Ereignis tritt ein
• ¬A ... das Ereignis tritt nicht ein
• P(A) = p ... Wahrscheinlichkeit für den Eintritt von A
• P(¬A) = 1 - p ... Wahrscheinlichkeit, dass A nicht eintritt

Dieses Experiment wird nun n-mal wiederholt - wir betrachten, wie oft sich das Ereignis A wiederholt und die damit zusammenhängende Wahrscheinlichkeit.
Beispiel: Wir würfeln 20 mal, wie oft kommt ein Sechser - wie hoch ist die Wahrscheinlichkeit, dass bei 20 Würfen 3 Sechser dabei sind etc.

Welche Funktionen bietet Maxima für derartige Berechnungen - welche Funktionen kann man sich leicht zurechtzimmern:

• binomial(n,k) ... eingebaute Maxima-Funktion für n!/(k!^.(n-k)!)
• binv(n,p,k) ... selbst definierte Funktion für die Anzahl P(k), mit der eine bestimmte Eigenschaft mit Wahrscheinlichkeit p k-mal auftritt. Sie wird über die Formel für "Ziehen mit Zurücklegen" bestimmt:
  
• binvert(n,p,a,b) ... meist wollen wir Bereiche wissen - "mindestens k-mal" oder "k zwischen a und b" - dies lässt sich (selbst definiert) wie folgt ausdrücken:
  

Beispiel

Bei einem Spielautomaten gewinnt man mit der Wahrscheinlichkeit 0.4. Mit welcher Wahrscheinlichkeit gewinnt man bei 100 Spielen:

* mindestens 50

* höchstens 30

* mindestens 30 - aber höchstens 40 Spiele

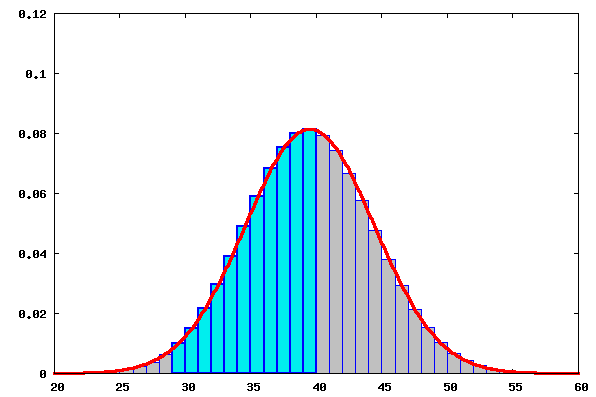
Wir wollen die Binomialverteilung durch eine geeignete Normalverteilung approximieren und anschließend beide Verteilungen grafisch darstellen.

des dritten Falls - mindestens 30, höchstens 40 Spiele

apply(draw2d,
  append([... Optionen ...],
         makeliste(rectangle(...))
  )
)	    

MAXIMA-Datei

Links:

• http://www.mathe-online.at/materialien/Franz.Kienast/files/Uebung_7_12_04/Binomialverteilung.ppt, Binomialverteilung, Günther Schwarz, Linz - Unterrichtsmaterialien auf mathe online