Maxima

Die gängigsten Funktionen, um mit Verteilungen zu arbeiten, sind in Maxima im Paket distrib enthalten. Für die Normalverteilung mit Erwartungswert μ und Standardabweichung σ stehen folgende Routinen bereit:

• pdf_normal(x,mu,sigma) ... beschreibt die Wahrscheinlichkeit für das Eintreten eines Einzelereignisses x einer normalverteilten Größe mit Erwartungswert μ und Standardabweichung σ.
• cdf_normal(x,mu,sigma) ... berechnet die Wahrscheinlichkeit für das Eintreten eines Ereignisses im Bereich zwischen -∞ und x (also die Fläche unter jener die Normalverteilung beschreibenden Dichtefunktion - einer Glockenkurve - zwischen -∞ und x).
• quantile_normal(phi,mu,sigma) ... berechnet jene Größe x, wo die Fläche der Normalverteilung zwischen -∞ und x den Wert phi annimmt - quasi die Umkehrung zu cdf_normal()!.

Beispiele:

• Berechnung der Wahrscheinlichkeit
• Berechnung eines Intervalls
• Berechnung des Erwartungswertes
• Berechnung der Standardabweichung

Die Lebensdauer von Fernsehröhren ist normalverteilt mit μ = 8.6 Jahre (Erwartungswert) und σ = 2.1 Jahre (Standardabweichung).

1. Stelle die Wahrscheinlichkeitsfunktion dar!
2. Wie groß ist die Wahrscheinlichkeit, dass eine Röhre höchstens 8 Jahre alt wird?
3. Wie groß ist die Wahrscheinlichkeit, dass eine Röhre mehr als 12 Jahre alt wird?
4. Wie groß ist die Wahrscheinlichkeit, dass eine Röhre zwsichen 5 und 15 Jahre alt wird?

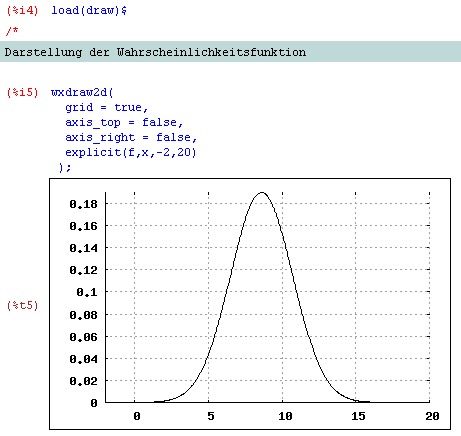
x ... Lebensdauer von Fernsehröhren in Jahren!

MAXIMA-Datei

Wir laden das Utility-File / Package distrib und geben geben die Kennwerte (μ, σ) ein. Anschließend wird eine Funktion der Wahrscheinlichkeitsdichte der Normalverteilung über den Befehl pdf_normal(x,μ,σ) generiert und die Funktion mit Hilfe des draw2d-Befehls geplottet (draw2d hat gegenüber plot2d Vorteile bei der Gestaltung, der Möglichkeit von Füllungen und gleichzeitigem Plot von mehreren verschiedenen Objekten, für die Verwendung muss das Package draw geladen werden).

Wir verwenden für die Fläche der Wahrscheinlichkeitsdichtefunktion die Maxima-Funktion cdf_normal(x,μ,σ).

Beantwortung der Fragestellungen:

Höchstens 8 Jahre alt	Mehr als 12 Jahre alt	zw. 5 und 15 Jahre alt
Die Wahrscheinlichkeit, dass eine Röhre höchstens 8 Jahre alt wird, beträgt immerhin über 38 Prozent.	Die Wahrscheinlichkeit, dass eine Röhre länger als 12 Jahre hält, beträgt knapp über 5 Prozent.	Die Wahrscheinlichkeit, dass eine Röhre zwischen 5 und 15 Jahre hält, beträgt über 95 Prozent.

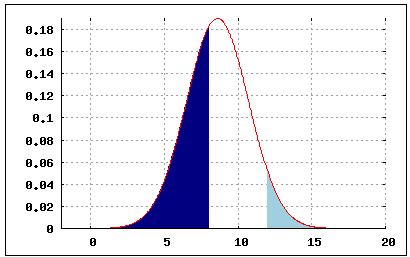
Darstellung - "höchstens 8 Jahre" (dunkelblau) und "mehr als 12 Jahre" (hellblau):

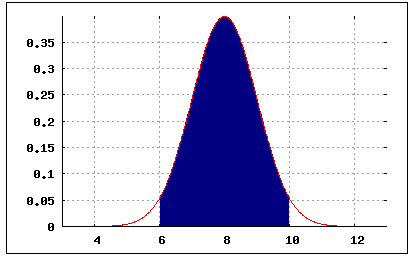
In welchem symmetrischen Intervall um den Erwartungswert μ = 8 Liter auf 100 km schwankt der Benzinverbrauch bei 95% der PKWs, wenn die Standardabweichung σ = 1 Liter pro 100 Kilometer beträgt?

x ... Benzinverbrauch in Liter!

Die Berechnung bedient sich der Formel für symmetrische Intervalle (Streubereiche) bei der Normalverteilung:
2^.Φ(z)-1 = P(Z)
Anschließend wird über den Befehl quantile_normal() von der Bereichswahrscheinlichkeit auf den entsprechenden Wert rückgerechnet und die Grenzen des Streubereichs bestimmt.

Probe: Antwort: Der Benzinverbrauch von 95% aller PKWs bewegt sich im Streubereich zwischen 6.04 und 9.96 Liter.

Darstellung des Streubereichs:

MAXIMA-Datei

Die Standardabweichung bei der Reißfestigkeit von Kettengliedern wird mit σ = 1200 Newton geschätzt. Wie groß muss der Erwartungswert μ mindestens sein, damit höchstens 1% der Kettenglieder eine Festigkeit von weniger als 10000 Newton besitzen?

x ... Reißfestigkeit in Newton

Um die Maxima-Funktion quantile_normal() optimal ausnützen zu können, ist die Verwendung der Standardnormalverteilung (μ=0, σ=1) günstig. Nach Berechnung des Zwischenergebnisses über diese wird auf die gegebenen Werte rückgerechnet. Wir bedienen uns dazu einer kleinen Hilfsfunktion, um diesen Vorgang nicht jedesmal durchführen zu müssen.

Anschließend berechnen wir den gesuchten Erwartungswert μ:

Probe:

Antwort: Der Erwartungswert μ für die Reißfestigkeit muss mindesten (ca.) 12790 Newton betragen, damit weniger als 1% aller Kettenglieder eine Reißfestigkeit unter 10000 Newton besitzen.

MAXIMA-Datei

Eine Waschmaschine soll für einen Waschgang mit einer vollen Ladung Wäsche durchschnittlich 70 Liter Wasser verbrauchen. Der Hersteller möchte erreichen, dass bei höchstens 3% aller verkauften Maschinen der Wasserverbrauch größer als 80 Liter ist. Welche Standardabweichung σ darf die Maschine (höchstens) haben, wenn man voraussetzt, dass der Wasserverbrauch normalverteilt ist?

x ... Verbrauch in Liter Wasser

Berechnung wieder über die Standardnormalverteilung mit einer eigenen Funktion:

MAXIMA-Datei

Links:

• http://home.schule.at/teacher/fruehwirth/8am/Skriptum%20-%20Normalverteilung.pdf, Volkshochschule Götzis - Abendgymnasium, Georg Frühwirth (Angaben zu den Übungsbeispielen)